10/08 - Mechanics of Convolution & Fourier Transform

Mechanics of the Convolution

Remember from the game:

Input	LTI System	Output	Reason
$\delta (t)$	$⟹$	$h(t)$	Given
$\delta (t-\lambda )$	$⟹$	$h(t-\lambda )$	Time Invarience
$x(\lambda )\delta (t-\lambda )$	$⟹$	$x(\lambda )h(t-\lambda )$	Proportionality
$x(t)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(\lambda )\delta (t-\lambda )dx$	$⟹$	$\underset{ConvolutionIntegral}{\underbrace{\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(\lambda )h(t-\lambda )dx}}$	Superposition

We will also denote the convolution as $x(t)*h(t)\equiv \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(\lambda )h(t-\lambda )dx$

Communative Property

$x(t)*h(t)$	$=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(\lambda )h(t-\lambda )d\lambda$	Let $t-\lambda =u$ thus $du=-d\lambda$
	$=-\underset{\mathrm{\infty }}{\overset{-\mathrm{\infty }}{\int }}x(t-u)h(u)du$	The order of integration switched due to changing from $-\lambda =u$
	$=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}h(u)x(t-u)du$
	$=h(t)*x(t)$

Example 1

$\delta (t)*x(t)$	$=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\delta (\lambda )x(t-\lambda )d\lambda$
	$=x(t)\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}d\lambda$
	$=x(t)$

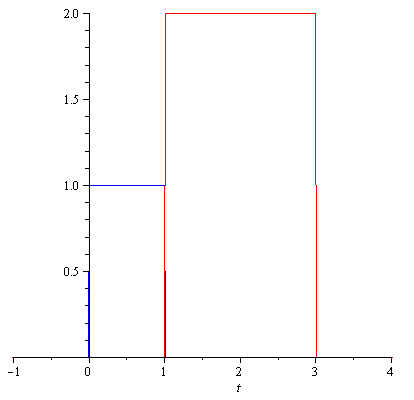
Example 2

$\stackrel{x(t)}{\overbrace{[u(t)-u(t-1)]}}*\stackrel{h(t)}{\overbrace{[u(t-1)-u(t-3)]}}=\{\begin{array}{ll}0,& t\le 1\\ \underset{0}{\overset{t-1}{\int }}1\cdot 2d\lambda ,& 1\le t\le 2\\ \underset{0}{\overset{1}{\int }}1\cdot 2d\lambda ,& 2\le t\le 3\\ \underset{t-3}{\overset{1}{\int }}1\cdot 2d\lambda ,& 3\le t\le 4\\ 0,& t>4\\ \end{array}=\{\begin{array}{ll}0,& t\le 1\\ 2t-2,& 1\le t\le 2\\ 2,& 2\le t\le 3\\ -2t-4,& 3\le t\le 4\\ 0,& t>4\\ \end{array}$

• In this case, we are doing the FSMI to $h(t)$
• If $u(t)$ isn't involved, then you can plug n chug with the integral. The u(t) will change the limits, which can be impractical to evaulate if you have more than 2.
• ? Does it matter which one you FSMI?

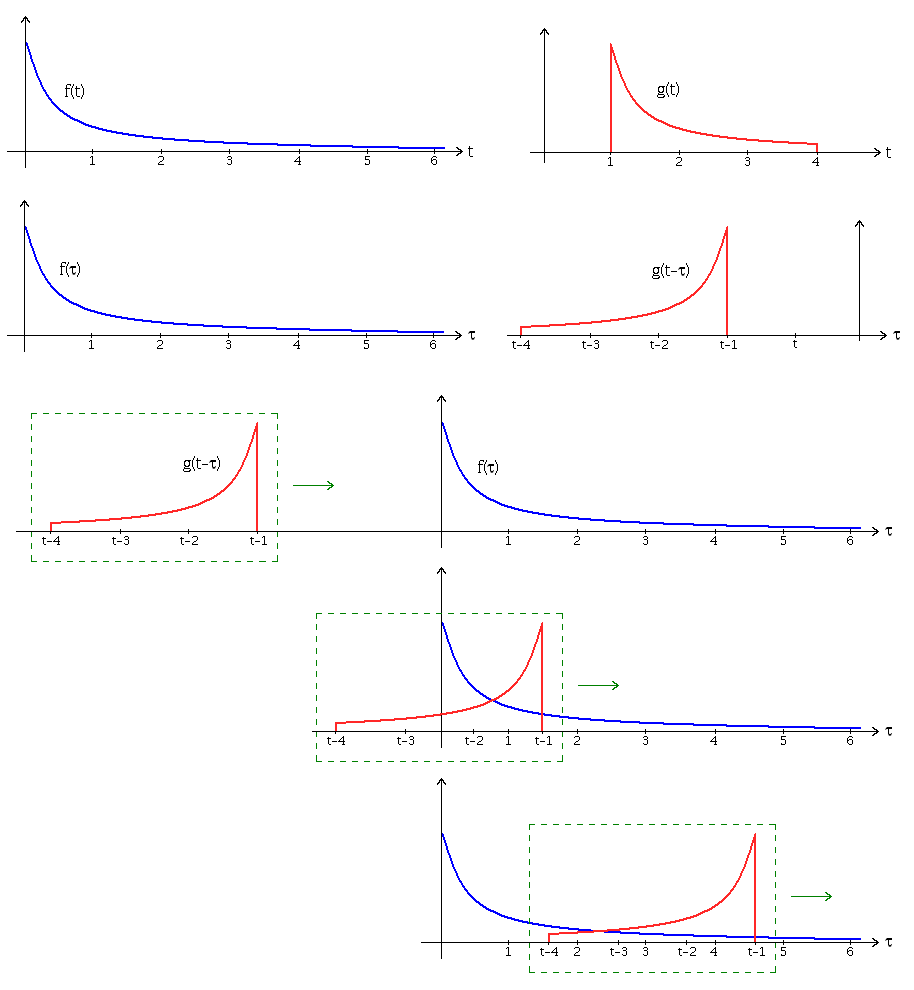
Convolution: A visual approach

• Flip: Flip one about the dependant axis
• Shift: The initial flipped function is at $t=0$. Shift this function for the multiply & integrate
• Multiply: Multiply the two functions
• Add/Integrate: You may need to make multiple equations for different intersections