Chapter 3 problems
Jump to navigation
Jump to search
3.9
Part A
- Using KVL:
- Thus the two points for the load line are and
- Overlay the above two points with the diode characteristics to find the answer.
Part B
- Thevenin Equivalent: and
- Using KVL: , thus and for the load line.
- can be read from the load line graph. We can then use this information to find the voltage over .
Part C
- KVL & KCL: and . Note that is the same thing as
- Thus and . Using the load line to find the I & V of device X. Then plug into the second equation to find
3.17
Part A
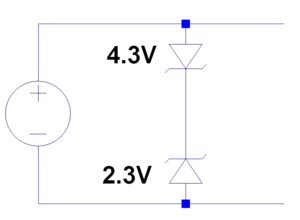
- Guessing D1 is on, D2 and D3 are off. Looking at the voltage drops, this is very unlikely.
- Guessing D1 off, D2 on, D3 off. and .
- Checking for positive current through presumed on diodes and negative voltage across the presumed off diodes.
- D1 and D2 fail. D3 passes.
- Guessing D1 and D2 on, D3 off.
- and . D1, D2, D3 pass.
Part B
- , : D1, D2, D3, D4 on.
- , : D1, D2, D3, D4 on.
- , : D2, D3 on. D1, D4 off.
- , : D2, D3 on. D1, D4 off.
- for
- for
- for
3.32
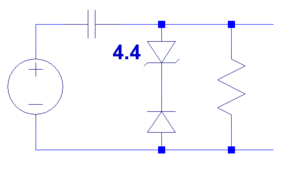
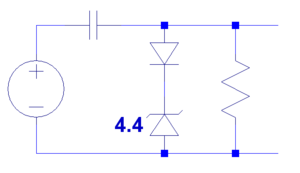
- How does this circuit work?