Magnetic Circuit

Author: John Hawkins

Problem Statement

Error creating thumbnail: File missing

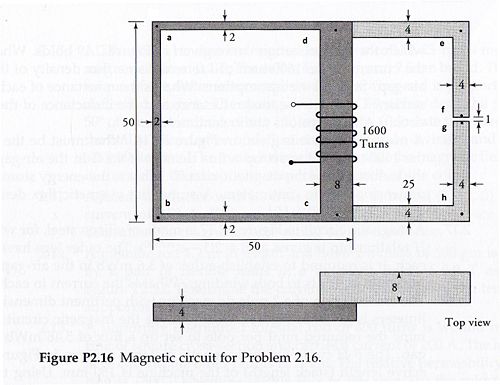
Problem 2.16 from Electric Machinery and Transformers, 3rd ed:

A magnetic circuit is given in Figure P2.16. What must be the current in the 1600-turn coil to set up a flux density of 0.1 T in the air-gap? All dimensions are in centimeters. Assume that magnetic flux density varies as

$B=[1.5H/(750+H)]$

.<ref>Guru and Huseyin, Electric Machinery and Transformers, 3rd ed. (New York: Oxford University Press, 2001), 129.</ref>

Solution

First, we note that the problem statement is incomplete. Assume that the core has a relative permeability of 500. Hence, for all magnetic sections excluding the air gap,

$\mu ={\mu }_r{\mu }_0=(500)(4\pi \times 10^{-7})=6.2832\times 10^{-4}$

Also, as recommended in the text, we will neglect fringing.

The lengths and areas of each of the sections to be evaluated are given in the following table.

Table 1: Lengths and Areas for the pertinent secions of the magnetic circuit.

Section	fg	def	ghc	dc	dabc
Length $l$ (m)	0.01	0.555	0.555	0.48	1.38
Area $A$ (m2)	0.0032	0.0032	0.0032	0.0096	8.0e-4

We must now work backward from the air-gap, since the value of the flux-density is given there. We need only employ the analagous equations to Ohm's Law, KVL, and KCL. All units are standard units.
Air Gap:

${{ℛ}}_{fg}=\frac{l_{fg}}{\mu A_{fg}}=4973.6$
${\mathrm{\Phi }}_{fg}=B_{fg}{A}_{fg}=3.20\times 10^{-4}$
${{ℱ}}_{fg}={{ℛ}}_{fg}{\mathrm{\Phi }}_{fg}=1.5915$

Right Arms:

${\mathrm{\Phi }}_{def}={\mathrm{\Phi }}_{ghc}={\mathrm{\Phi }}_{fg}=3.20\times 10^{-4}$
${{ℛ}}_{def}={{ℛ}}_{ghc}=\frac{l_{def}}{\mu A_{def}}=2.7603\times 10^5$
${{ℱ}}_{def}={{ℱ}}_{ghc}={{ℛ}}_{def}{\mathrm{\Phi }}_{def}=88.331$

Center Column:

${{ℱ}}_{dc}={{ℱ}}_{def}+{{ℱ}}_{fg}+{{ℱ}}_{ghc}=178.25$
${{ℛ}}_{dc}=\frac{l_{dc}}{\mu A_{dc}}=79,577$
${\mathrm{\Phi }}_{dc}=\frac{{{ℱ}}_{dc}}{{{ℛ}}_{dc}}=0.0022$

Left Arm:

${\mathrm{\Phi }}_{dabc}={\mathrm{\Phi }}_{dc}-{\mathrm{\Phi }}_{def}=0.0019$
${{ℛ}}_{dabc}=\frac{l_{dabc}}{\mu A_{dabc}}=2.745\times 10^6$
${{ℱ}}_{dabc}={{ℱ}}_{dabc}{\mathrm{\Phi }}_{dabc}=5,271.2$

Conclusions:

${{ℱ}}_{Total}={{ℱ}}_{dabc}+{{ℱ}}_{dc}+{{ℱ}}_{def}+{{ℱ}}_{fg}+{{ℱ}}_{ghc}=5,627.7$
$\mathbf{i}\mathbf{=}\frac{{{ℱ}}_{Total}}{N}\mathbf{=}\mathbf{3}\mathbf{.}\mathbf{5}\mathbf{2}\mathbf{A}$

Which is the quantity we were looking for.

Calculations were performed using the following Magnetic Circuit Matlab Script.

References

<references />

Reviewed By

Amy Crosby

Kirk Betz