The Class Notes

The following are the notes as interpreted by Kirk Betz from ENGR 431 taught by Dr. Rob Frohne. Electrical Magnetic Conversion is the study of magnetic circuits in all there forms.

Notes for reviewer Be sure all 'l' have been replaced with $\ell$

EMEC Notes

January 4, 2010

Introduction to EMEC

Syllabus was handed out and an outline of the class structure what introduce. We where also briefed on what we would be talking about his quarter.

Magnetic Circuits

January 6 2010

From circuits we know that V is a function of the E field.

$$\begin{gathered} V \\ =\int ed\ell \end{gathered}$$

The E field moves along a closed path of length $\ell$. By integrating E along the path $\ell$ we find the Voltage V as shown in the above equation.

integrated the e field along the path

$$\begin{gathered} \overrightarrow{F} \\ =q\overrightarrow{v}\times \overrightarrow{B} \end{gathered}$$

$$\begin{gathered} d\overrightarrow{F} \\ =Id\overrightarrow{\ell }\times \overrightarrow{B} \end{gathered}$$

${ℱ}=H{\ell }_1+H{\ell }_2$

$$\begin{gathered} V \\ =R_{1}I+R_{2}I \end{gathered}$$

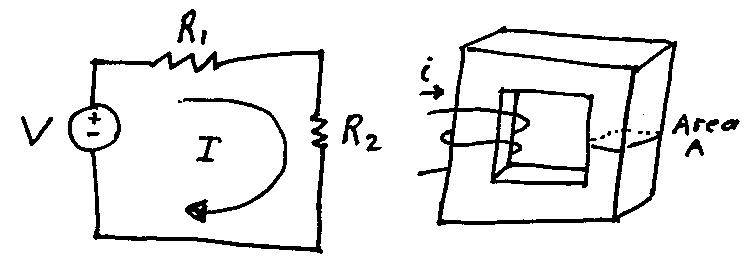
Picture drawn by Kirk Betz based on drawing by Dr. Frohnes, lecture Jan. 6, 2010

Magnetic Equations

$\int \overrightarrow{H}d\overrightarrow{\ell }={ℱ}$

$\oint \overrightarrow{H}d\overrightarrow{\ell }=Ni=\sum _{n}H\ell +Ni=0$

$\oint \overrightarrow{B}d\overrightarrow{s}=0$

$$\begin{gathered} \int \overrightarrow{B}d\overrightarrow{s}=\varphi \approx B{A}_{rea} \\ Magnetic \\ Flux \end{gathered}$$

$$\begin{gathered} {ℛ}\equiv Reluctance \\ \frac{{ℱ}}{\varphi }=\frac{Ni}{\varphi } \end{gathered}$$

$$\begin{gathered} \overrightarrow{B}=\mu \overrightarrow{H} \\ Assumes \\ Linearity \end{gathered}$$

${ℛ}\frac{\ell }{\mu A}$

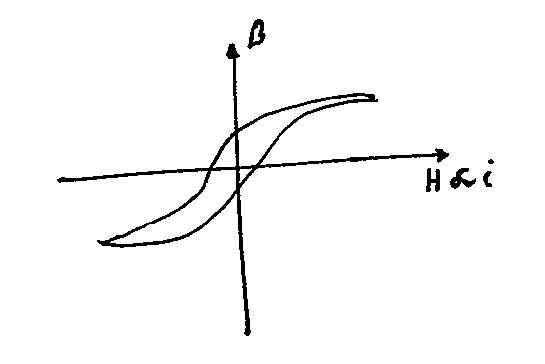
Picture drawn by Kirk Betz based on drawing by Dr. Frohnes, lecture Jan. 6, 2010

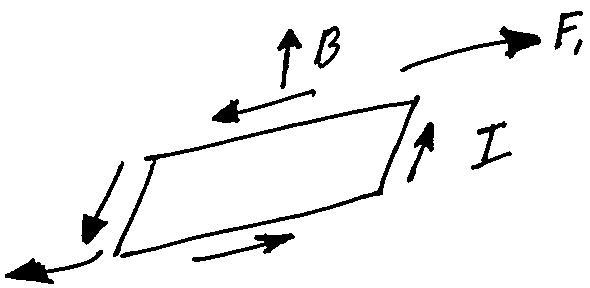
Pictures drawn by Kirk Betz based on drawing by Dr. Frohnes, lecture Jan. 6, 2010

Magnetic Circuits Examples

What about chancing currents, etc.?

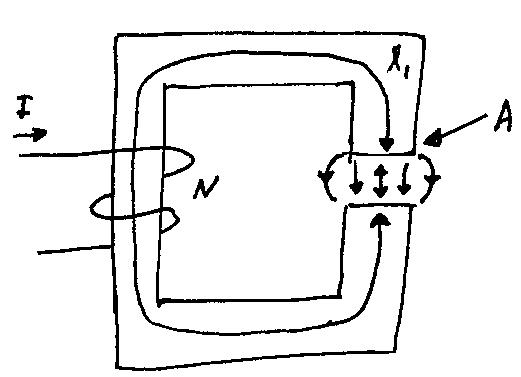
Picture drawn by Kirk Betz based on drawing by Dr. Frohnes, lecture Jan. 8, 2010

$\oint \overrightarrow{H}d\overrightarrow{\ell }=Ni$

Case i)

$$\begin{gathered} \mu =10^4{\mu }_0 \\ in \\ the \\ core \end{gathered}$$ Something about this part doesn't seem right.

$$\begin{gathered} Find \\ \overrightarrow{B} \\ in \\ the \\ gap. \end{gathered}$$

Graph and picture 6

$$\begin{gathered} H\ell \\ =NI \end{gathered}$$, $$\begin{gathered} I \\ \propto H \end{gathered}$$

$$\begin{gathered} NI \\ ={ℱ}\backsim V \end{gathered}$$

${ℛ}=\frac{\ell }{\mu A}\backsim R=\frac{\ell }{\sigma A}$

$$\begin{gathered} \varphi \\ =BA\backsim I=JA \end{gathered}$$

$R_c=\frac{{\ell }_1}{\mu A}$

$R_g=\frac{g}{{\mu }_0(\sqrt{A}+g{)}^2}$

$$\begin{gathered} \varphi \\ =B(\sqrt{A}+g{)}^2=\frac{NI}{R_g+R_c} \end{gathered}$$

$B_g\frac{NI}{(R_g+R_c)(\sqrt{A}+g{)}^2}$

Magnetic Circuits Continued

jan 11, 2010

some random graph here, can't really read it.

Case ii) Include non-linearity & find B in the Gap

$\oint \overrightarrow{H}d\overrightarrow{\ell }=NI=H{\ell }_1+H_g=H({\ell }_1+g)$

$$\begin{gathered} \varphi \\ =\int \overrightarrow{B}d\overrightarrow{s}=BA \end{gathered}$$

picture 7 goes here

$$\begin{gathered} \varphi \\ =\frac{NI-H{\ell }_1}{R_g}=\frac{-1}{R_g}(H{\ell }_1)+\frac{NI}{R_g} \end{gathered}$$ not sure about the -1 here

What energy is list in the hysteresis loop?

$$\begin{gathered} P \\ =vi \end{gathered}$$

$$\begin{gathered} W \\ =\int Pdt \end{gathered}$$

$$\begin{gathered} \oint \overrightarrow{E}d\overrightarrow{\ell }=\frac{-d}{dt}\int \overrightarrow{B}d\overrightarrow{s}Farada{y}^{\prime }s \\ Law \end{gathered}$$

hmm check these

$\overrightarrow{E}=\frac{J}{\sigma }$

$$\begin{gathered} \lambda \\ =Li \end{gathered}$$

e is voltage

$e=\frac{d\lambda }{dt}=L\frac{di}{dt}$

$$\begin{gathered} \lambda \\ =N\varphi \end{gathered}$$

$$\begin{gathered} N\equiv number \\ of \\ turns \end{gathered}$$

$\varphi \equiv Flux$