Chapter 22--Fourier Series: Fundamental Period, Frequency, and Angular Frequency: Difference between revisions
Andrew.roth (talk | contribs) (New page: Please refrain from error checking until the 2 reviewers do their job. Thank you! I can't figure out how to reference something. If someone knows how please let me know. Thanks! ==Per...) |
John.hawkins (talk | contribs) No edit summary |
||
| (16 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
22 lines (currently) |
|||
Please refrain from error checking until the 2 reviewers do their job. Thank you! |
|||
1 reference |
|||
I can't figure out how to reference something. If someone knows how please let me know. Thanks! |
|||
1 figure |
|||
123 points |
|||
==Period, Frequency, and Angular Frequency== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
Long long ago, in a high school class called trigonometry, we leaned about '''periodic functions'''. A periodic function is a function that repeats itself over and over for infinity. The '''period''' of the function is the distance of one iteration that is infinitely repeating. |
Long long ago, in a high school class called trigonometry, we leaned about '''periodic functions'''. A periodic function is a function that repeats itself over and over for infinity. The '''period''' of the function is the distance of one iteration that is infinitely repeating. |
||
A signal <math>f(t)</math> is periodic if, for some <math>T > 0</math> and all ''t'', |
<center>A signal <math>f(t)</math> is periodic if, for some <math>T > 0</math> and all ''t'',</center> |
||
<math>f(t+T) = f(t)</math><ref> |
<center><math>f(t+T) = f(t)</math><ref>DeCarlo/Lin, Linear Circuit Analysis--Time Domain, Phasor, and Laplace Transform Approaches, Second Edition. Figure 22.1</ref></center> |
||
Where T is the period |
|||
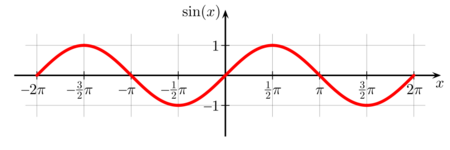
The picture to the right shows the plot of the standard sine function whose period is <math>2\pi</math>. What the plot does not show is that the line keeps extending and repeating the bumps and valleys over the whole x axis, or <math>(-\infty,\infty)</math>. But wait! Can't the period also be <math>4\pi</math> or <math>6\pi</math>? In fact it can. Because the graph of sin(x) repeats itself every <math>2\pi</math> units, the period of the function is actually <math>2\pi n</math> where n is any whole number from zero to <math>\infty</math> |
The picture to the right shows the plot of the standard sine function whose period is <math>2\pi</math>. What the plot does not show is that the line keeps extending and repeating the bumps and valleys over the whole x axis, or <math>(-\infty,\infty)</math>. But wait! Can't the period also be <math>4\pi</math> or <math>6\pi</math>? In fact it can. Because the graph of sin(x) repeats itself every <math>2\pi</math> units, the period of the function is actually <math>2\pi n</math> where n is any whole number from zero to <math>\infty</math> |
||
===Frequency and Angular Frequency=== |
|||
| ⚫ | |||
{{reflist}} |
|||
The '''Frequency''' is the number of periods per second and is defined mathematically as |
|||
<math>f = \frac{1}{T}</math> |
|||
The standard unit of measurement for frequency is Hz (Hertz). 1 Hz = 1 cycle/second |
|||
The '''Angular Frequency''' is defined as |
|||
<math>\omega = 2\pi f = \frac{2\pi}{T}</math> |
|||
The standard unit of measurement for angular frequency is in radians/second. |
|||
===Fundamental Period, Frequency, and Angular Frequency=== |
|||
The '''fundamental period''' is the smallest positive real number <math>T_0</math> for which the periodic equation <math>f(t+T) = f(t)</math> holds true. |
|||
The '''fundamental frequency''' is defined as <math>f_0 = \frac{1}{T_0}</math>. |
|||
The '''fundamental angular frequency''' is defined as <math>\omega_0 = 2\pi f_0 = \frac{2\pi}{T_0}</math>. |
|||
| ⚫ | |||
<references /> |
|||
==Author== |
|||
Andrew Roth |
|||
==Reviewers== |
|||
Brandon Vazquez |
|||
Ben Blackley |
|||
==Readers== |
|||
Thomas Wooley |
|||
Jaymin Joseph |
|||
John Hawkins |
|||
Latest revision as of 03:30, 20 January 2010
22 lines (currently)
1 reference
1 figure
123 points
Period, Frequency, and Angular Frequency
Period
Long long ago, in a high school class called trigonometry, we leaned about periodic functions. A periodic function is a function that repeats itself over and over for infinity. The period of the function is the distance of one iteration that is infinitely repeating.
Where T is the period
The picture to the right shows the plot of the standard sine function whose period is . What the plot does not show is that the line keeps extending and repeating the bumps and valleys over the whole x axis, or . But wait! Can't the period also be or ? In fact it can. Because the graph of sin(x) repeats itself every units, the period of the function is actually where n is any whole number from zero to
Frequency and Angular Frequency
The Frequency is the number of periods per second and is defined mathematically as
The standard unit of measurement for frequency is Hz (Hertz). 1 Hz = 1 cycle/second
The Angular Frequency is defined as
The standard unit of measurement for angular frequency is in radians/second.
Fundamental Period, Frequency, and Angular Frequency
The fundamental period is the smallest positive real number for which the periodic equation holds true.
The fundamental frequency is defined as .
The fundamental angular frequency is defined as .
References
<references />
Author
Andrew Roth
Reviewers
Brandon Vazquez
Ben Blackley
Readers
Thomas Wooley
Jaymin Joseph
John Hawkins













