Chapter 22--Fourier Series: Fundamental Period, Frequency, and Angular Frequency
Under Construction
Please refrain from error checking until the 2 reviewers do their job. Thank you!
I can't figure out how to reference something. If someone knows how please let me know. Thanks!
Period
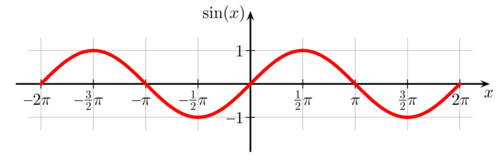
Long long ago, in a high school class called trigonometry, we leaned about periodic functions. A periodic function is a function that repeats itself over and over for infinity. The period of the function is the distance of one iteration that is infinitely repeating.
A signal is periodic if, for some and all t,
<ref>Textbook, 22.1</ref>
The picture to the right shows the plot of the standard sine function whose period is . What the plot does not show is that the line keeps extending and repeating the bumps and valleys over the whole x axis, or . But wait! Can't the period also be or ? In fact it can. Because the graph of sin(x) repeats itself every units, the period of the function is actually where n is any whole number from zero to