Chapter 22--Fourier Series: Fundamental Period, Frequency, and Angular Frequency
Before you read anything, please make sure you "Always render PNG" in My Preferences/Math.
22 lines (currently)
1 reference
1 figure
123 points
Please refrain from error checking until the 2 reviewers do their job. Thank you!
I can't figure out how to reference something. If someone knows how please let me know. Thanks!
Period, Frequency, and Angular Frequency
Period
Long long ago, in a high school class called trigonometry, we leaned about periodic functions. A periodic function is a function that repeats itself over and over for infinity. The period of the function is the distance of one iteration that is infinitely repeating.
Where T is the period
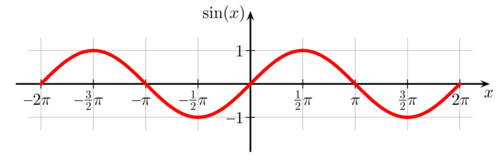
The picture to the right shows the plot of the standard sine function whose period is . What the plot does not show is that the line keeps extending and repeating the bumps and valleys over the whole x axis, or . But wait! Can't the period also be or ? In fact it can. Because the graph of sin(x) repeats itself every units, the period of the function is actually where n is any whole number from zero to
Frequency and Angular Frequency
The Frequency is the number of periods per second and is defined mathematically as
The standard unit of measurement for frequency is Hz (Hertz). 1 Hz = 1 cycle/second
The Angular Frequency is defined as
The standard unit of measurement for angular frequency is in radians/second.
Fundamental Period, Frequency, and Angular Frequency
The fundamental period is the smallest positive real number for which the periodic equation holds true.
The fundamental frequency is defined as .
The fundamental angular frequency is defined as .
References
Author
Andrew Roth