Signals and Systems: Difference between revisions
Daniel.liwag (talk | contribs) |
Brian.Clark (talk | contribs) |
||
| Line 150: | Line 150: | ||
==People Involved with this Wiki== |
==People Involved with this Wiki== |
||
===2013-2014 Contributors=== |
|||
[[Brian Clark]] |
|||
===2012-2013 Contributors=== |
===2012-2013 Contributors=== |
||
Revision as of 12:42, 18 December 2013
Topics
Overview of Signals and Systems
Individual Subjects
- Linear Time Invariant Systems
- Orthogonal Functions
- Finding the Energy in a Signal
- Fourier Series
- Fourier Transforms
- Sampling
- FIR Filter Example
- Relationship between e, sin and cos
- Multirate Filtering
Some Useful Links to Suppliment or Substitute for a Textbook
Books on Signal Processing
- Spectral Audio Signal Processing, by Julius O. Smith III
- The Scientist and Engineer's Guide to Digital Signal Processing by Steven W. Smith, Ph.D. The professor likes this one.
- Discrete Time Signals & Systems
- The Fast Fourier Transform by E. O. Brigham This was one of the professor's textbooks when he took this class.
- Mathematics of Signal Processing: A First Course, by Charles L. Byrne Good chapters on Computer Aided Tomography (CAT Scan) as well as a lot of other interesting things.
Fourier Series
- Interactive Mathematics (like a textbook with some examples)
- Mathworld
- Wikipedia
- MIT handout on Fourier Series, Fourier Transform, and Laplace Transform
- Fourier Theory B..M..N.. Clarke
Dirac Delta Function and Convolution
Multi-rate Filtering
Multirate Filters Introduction
Slides from a Presentation on Polyphase Decimation and Interpolation by Mark Fowler
FIR Filters
- Fast Convolution Based on the FFT This reference shows how end effects are dealt with. To use the FFT for convolution, you need to do it in blocks, which leads to end effects, and more latency, but if your blocks are big enough, it speeds up the convolution.
- The truncated Fourier series or DFT method of FIR filter design gives the best approximation of the desired frequency response in a least squared error sense, but it is not very good near discontinuities. The Parks-McClellan (Remez) iterative algorithm gives equal ripple in the pass band and stop band. This is the best in terms of minimizing the maximum error in each area, which is usually better in the real world. MATLAB/octave have automated functions to do that. See remez() in the Signals package of octave.
- A nice detailed description of the Parks McClellan algorithm with MATLAB/octave code.
Adaptive FIR Filters
Introduction to Adaptive Filters, Simon Haykin
Adaptive Filters In the Frequency Domain
Adaptive Filter Echo Cancellation
Adaptive Filters and Applications (Mathworks)
More Applications of Adaptive Filters
Constant Modulus Algorythm
Using the CMA on antenna arrays
Course Pages
Class notes for Signals & Systems
Articles
Octave Tutorials
Installing Octave on a Mac (Chris Lau)
Octave and Scilab on a Mac (Ben Henry)
Installing Octave (with the GUI) from source on Ubuntu
ASN2 - Octave Tutorial (Jodi S. Hodge)
FIR Filter Example Code for Octave
FIR Filter Design and Testing Using the DFT
Interpolation using the DFT Example Script
An example showing how convolution is just a dot product
Tuner Upper Removal Demonstration
Airplane Noise Removal Demonstration
Final Project (2011)
morse.m This is the one from mathworks
Table of Fourier Transform Properties
Homework Assignments
Please put your name next to the assignment, linking it to your submission
- HW #1 - Make a personal page on this wiki (Chris Lau)(Jodi S. Hodge)(Chris Wills)(Victor Shepherd)
- HW #2 - Write a tutorial about installing and/or using Octave (Chris Lau)(Jodi S. Hodge)(Victor Shepherd)
- HW #3 - Show graphically that (Chris Lau)(Jodi S. Hodge)(Chris Wills)(Victor Shepherd)
- HW #4 - Given a linear time-invariant system where produces an output , find the output due to any function (Chris Lau)
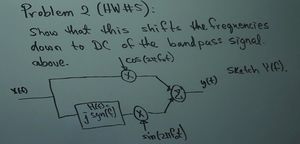
- HW #5: (Chris Lau)
- Part 1 - Find and relate it to the Laplace Transform. Derive the Inverse Laplace Transform of this from the inverse Fourier Transform.
- Part 2 -
- HW #6 - Pick a property of the Fourier Transform & present it on the Wiki. Make a table with all your properties. Interpret your property. (Ben Henry)(Chris Lau)(Victor Shepherd)
- HW #7 - Finish the practice tests
- HW #8 - Make a page about interpolating FIR filters. Note how many multiply/add operations.(Jodi S. Hodge)(Chris Lau)(Victor Shepherd)
- HW #9 - Add to #8 writeup how to do a decimating filter and figure out how many multiply & adds are needed for a n/2 decimating low pass filter.(Jodi S. Hodge)(Chris Lau)(Victor Shepherd)
- HW #10 - Use Octave (or Mathlab or Silab) to plot the frequency response of low pass filters with cut off frequencies of 1/32T, 1/8T, and 1/4T and compare how many coeffficients are needed with an eye to answer the question "Is it less calculation to decimate and then filter, or better to put the filter in the pre-decimation filter?" (Jodi S. Hodge)(Victor Shepherd)
- HW #11 - Is our method the same as Mark Fowler's? See
Wiki. Same # multiply and adds? See Notes 11/3/10. (Jodi S. Hodge)(Victor Shepherd)
- HW #12 - Experiment with a variety of signals having a 3Khz bandwidth to determine the resolution you can get when doing a cross correlation . You can generate the signals randomly and filter them to obtain the band-limited signals. (Jodi S. Hodge)
- HW #13 - Derive the following realtions:
- a)
- b)
- c) (Victor Shepherd)
- HW #14 - Come up with a use for an adaptiveFIR filter and make an Octave script to demonstrate it. (Jodi S. Hodge)(Victor Shepherd)
- HW #15 - Do Practice Exam II (Victor Shepherd)
- CW-Robot Octave Simulation




![{\displaystyle {\mathcal {F}}[e^{-\sigma t}x(t)u(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fff13c3c7a479f107c9e90e0aed1908dd4a969ce)