Using Nonlinear Circuits as RF Mixers

Because nonlinear circuits can shift the frequencies of a linear combination of sinusoidal inputs (see this notebook, this can be used as a frequency shifting mechanism. This great video shows how that works in real life.

The trick to making a good mixer is to find the best nonlinear way of combining the local oscillator signal and the radio frequency signal to produce as much as possible only the RF signal shifted by the local oscillator frequency. Since we want an output frequency of $\omega_{lo} - \omega_{rf}$, the simplist way to nonlinearly combine the local oscillator with the RF signal would be to multiply them.

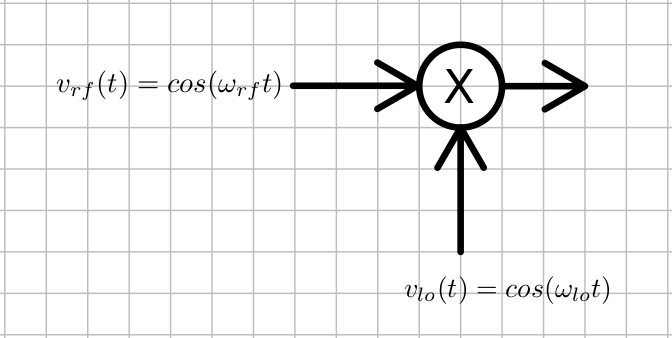
This is because $cos(\omega_{lo}t) cos(\omega_{rf}t) = (cos[(\omega_{rf} + \omega{lo})t] + cos[(\omega_{lo}-\omega_{rf})t])/2$. Unfortunately, it is very difficult to make a circuit that actually does mulitplication well, so we have to go fishing around for other ways of combining the two signals. This multiplication seemed to work really well. What if we used some switches to switch the RF signal in time with the local oscillator. The idea is we make the local oscillator control switches that make a signal that is the RF signal multiplied by a square wave with the period of the local oscillator. $$v_o(t) = v_{rf}(t) sgn(v_{lo}(t))$$ We could make $sgn(v_{lo}(t))$ using a high gain amplifier with clipping at the power supply limits, and use that square wave to control semiconductor switches that do the mmultiplication. This produces a lot more distortion signals than we want, but hopefully we can ignore or filter out undesired ones.