Laplace transforms: R series with RC parallel circuit: Difference between revisions
Jump to navigation
Jump to search
(New page: ===Problem Statement=== v(0)=0 Volts v(t)=10 Volts R1=20 Ohm R2=30 Ohm C=.1 Farad) |
|||
| (64 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
===Problem Statement=== |
===Problem Statement=== |
||
v(0)=0 Volts |
|||
:Find the Voltage across the capacitor for t>=0: |
|||
v(t)=10 Volts |
|||
R1=20 Ohm |
|||
:Capacitor is uncharged at t(0-) |
|||
R2=30 Ohm |
|||
C=.1 Farad |
|||
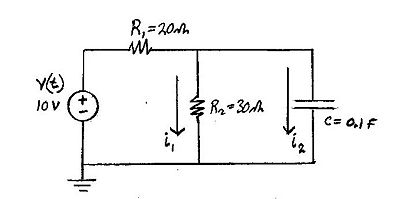
[[Image:lna_hw_5.jpg|400px|thumb|left|Fig (1)]] |
|||
: <math>v(t0-)=0 Volts\,</math> |
|||
: <math>v(t)=10 Volts\,</math> |
|||
: <math>R_1=20 \boldsymbol{\Omega}\,</math> |
|||
: <math>R_2=30 \boldsymbol{\Omega}\,</math> |
|||
: <math>C=.1 Farad\,</math> |
|||
'''Voltage equations:''' |
|||
:equation 1 |
|||
:<math>v(t)=R1(i_1+i_2)+R2(i_1)\,</math> |
|||
:<math>10=20(i_1+i_2)+30(i_1)\,</math> |
|||
:<math>i_1=(10-20i_2)/50\,</math>___________________________________equation (1) |
|||
:equation 2 |
|||
:<math>v(t)=R1(i_1+i_2)+\dfrac{1}{C}\int{i_2 dt}\,</math> |
|||
:<math>10=20(i_1+i_2)+\dfrac{1}{.1}\int{i_2 dt}\,</math>_______________________equation (2) |
|||
'''Solve equations (1) and (2) simultaneously''' |
|||
:Substituting equation (1) into equation (2) gives... |
|||
:<math>20((10-20i_2)/50+i_2)+\dfrac{1}{.1}\int{i_2 dt}=10\,</math> |
|||
:simplifies to... |
|||
:<math>12i_2+10\int{i_2 dt}=6\,</math> |
|||
'''Take the Laplace Transform to move to the S-domain''' |
|||
:<math>\mathcal{L}\left\{\int_{0-}^\infty{(i_2) dt}\right\}=I_2/s\,</math> |
|||
:<math>\mathcal{L}\left\{(1)\right\}=1/s\,</math> |
|||
:<math>12I_2+10I_2/S=6/S\,</math> |
|||
:<math>I_2(12+10/S)=6/S\,</math> |
|||
:<math>I_2=6/(12S+10)\,</math> |
|||
:<math>I_2=(1/2)(1/(S+(5/6))\,</math> |
|||
'''Take the inverse Laplace transform to move back into the t-domain''' |
|||
:<math>i_2=(1/2)(e^{-(5/6)t})\,</math> |
|||
:substitute this equation back into equation (1) |
|||
:<math>i_1=(10-20(.5e^{-(5t/6)}))/50\,</math> |
|||
:<math>i_1=(1/5)(1-e^{-(5t/6)})\,</math> |
|||
'''Voltage on Capacitor''' |
|||
:<math>v_{capacitor}=10/20(i_1+i_2)\,</math> |
|||
:<math>v_{capacitor}=10-20((1/5)(1-e^{-(5t/6)})+(1/2)(e^{-(5t/6)}))\,</math> |
|||
:<math>v_{capacitor}=10-4+4e^{-(5t/6)}-10e{-(5t/6)}\,</math> |
|||
===Answer=== |
|||
::<math>v_{capacitor}=6-6e^{-(5t/6)}\,</math> Volts |
|||
---- |
|||
===Apply the Initial and Final Value Theorems to find the initial and final values=== |
|||
:'''Initial Value Theorem''' |
|||
::<math>\lim_{s\rightarrow \infty} sF(s)=f(0)\,</math> |
|||
:'''Final Value Theorem''' |
|||
::<math>\lim_{s\rightarrow 0} sF(s)=f(\infty)\,</math> |
|||
:<math>V(S)=6/s-6(1/(s+(5/6))\,</math> |
|||
:'''Initial Value:''' |
|||
::<math>\lim_{s\rightarrow \infty} sV(s)=6s/s-6s(1/(s+(5/6))\,</math> |
|||
::<math>\lim_{s\rightarrow \infty} sV(s)=0\,</math> |
|||
:::Initial Value = 0 Volts |
|||
:'''Final Value:''' |
|||
::<math>\lim_{s\rightarrow 0} sV(s)=6s/s-6s(1/(s+(5/6))\,</math> |
|||
::<math>\lim_{s\rightarrow 0} sV(s)=6\,</math> |
|||
:::'''''Final Value = 6 Volts''''' |
|||
:<math>v(t0)=0\,</math> Volts |
|||
:<math>v(t{\infty})=6\,</math> Volts |
|||
===Bode Plot=== |
|||
'''T-domain''' |
|||
:<math>V_{in}(t)=10\,</math> |
|||
:<math>V_{out}(t)=6-6*e^-((5/6)t)\,</math> |
|||
'''S-domain''' |
|||
:<math>V_{in}(s)=10/s\,</math> |
|||
:<math>V_{out}(s)=6/s -6(1/(s+5/6))\,</math> |
|||
'''Transfer Function''' |
|||
:<math>H(S)=V(s)_{out}/V(s)_{in}\,</math> |
|||
:<math>H(S)=3/(6s+5)\,</math> |
|||
'''Bode Plot''' |
|||
[[Image:Bode plot oct30.JPG|700px|thumb|left|Fig (1)]] |
|||
---- |
|||
===How to use break points and asymptotes to obtain the magnitude frequency response of the system...=== |
|||
The break points are the values of s in H(s) that make the numerator and or the denominator 0. |
|||
The location of the break points determines the magnitude frequency response of the system at that frequency. |
|||
Zeros are where the numerator is equal to zero. |
|||
Poles are when the denominator is equal to zero. |
|||
===Use Convolution to find the output of the system=== |
|||
:<math>H(S)=3/(6s+5)\,</math> |
|||
:<math>h(t)=\mathcal{L}^{-1}\left\{(3/(6s+5))\right\},\,</math> |
|||
:<math>h(t)=(1/2)*e^{-5t/6}\,</math> |
|||
:<math>v(t)=v(t)*h(t)=\int_{0}^{t}{v(\tau)h(t-\tau)d\tau}\,</math> |
|||
:<math>v(t)=\int_{0}^{t}{(10)((1/2)e^{(-5/6)(t-\tau)})d\tau}\,</math> |
|||
:<math>v(t)=6-6e^{-5t/6}\,</math> |
|||
===State Example=== |
|||
For the voltage on the capacitor... |
|||
<math>\begin{bmatrix} (dv/dt) v_c \end{bmatrix}=\begin{bmatrix} -R1/C \end{bmatrix} \begin{bmatrix} (i_2+i_3) \end{bmatrix} + \begin{bmatrix} 1/C \end{bmatrix} \begin{bmatrix} V(t) \end{bmatrix}</math> |
|||
<math>\begin{bmatrix} (dv/dt) v_c \end{bmatrix}=\begin{bmatrix} -200 \end{bmatrix} \begin{bmatrix} (i_2+i_3) \end{bmatrix} + \begin{bmatrix} 100 \end{bmatrix} \begin{bmatrix} V(t) \end{bmatrix}</math> |
|||
---- |
|||
Written by: Andrew Hellie |
|||
Checked by: Kendrick Mensink |
|||
Latest revision as of 20:17, 30 November 2009
Problem Statement
- Find the Voltage across the capacitor for t>=0:
- Capacitor is uncharged at t(0-)
Voltage equations:
- equation 1
- ___________________________________equation (1)
- equation 2
- _______________________equation (2)
Solve equations (1) and (2) simultaneously
- Substituting equation (1) into equation (2) gives...
- simplifies to...
Take the Laplace Transform to move to the S-domain
Take the inverse Laplace transform to move back into the t-domain
- substitute this equation back into equation (1)
Voltage on Capacitor
Answer
- Volts
Apply the Initial and Final Value Theorems to find the initial and final values
- Initial Value Theorem
- Final Value Theorem
- Initial Value:
- Initial Value = 0 Volts
- Final Value:
- Final Value = 6 Volts
- Volts
- Volts
Bode Plot
T-domain
S-domain
Transfer Function
Bode Plot
How to use break points and asymptotes to obtain the magnitude frequency response of the system...
The break points are the values of s in H(s) that make the numerator and or the denominator 0.
The location of the break points determines the magnitude frequency response of the system at that frequency.
Zeros are where the numerator is equal to zero.
Poles are when the denominator is equal to zero.
Use Convolution to find the output of the system
State Example
For the voltage on the capacitor...
Written by: Andrew Hellie
Checked by: Kendrick Mensink