|
|
| Line 93: |
Line 93: |
|
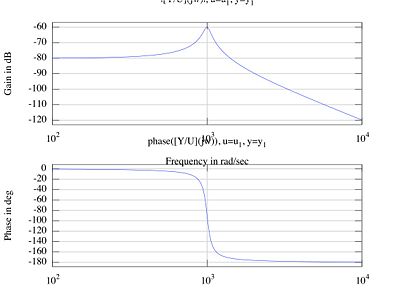
Looking at the top part of the Bode plot, we see that the graph is indeed going down at roughly 40db/decade at 1000. |
|
Looking at the top part of the Bode plot, we see that the graph is indeed going down at roughly 40db/decade at 1000. |
|
|
|
|
|
|
===Convolution=== |
|
|
|
|
|
We now want to show how convolution can achieve the same result as our Laplace Transform methods. |
|
|
|
|
|
Convolution means that |
|
|
|
|
|
<math>i(t)=v(t)*h(t)=\int_{0}^{t}{v(\tau)h(t-\tau)d\tau}</math> |
|
|
|
|
|
where <math>h(t)</math> is the inverse Laplace transform of the transfer function. |
|
|
|
|
|
Here, |
|
|
|
|
|
<math>h(t)=0.1e^{-2500t}sin(998.7t) \,</math> |
|
|
|
|
|
Thus, |
|
|
|
|
|
<math>i(t)=\int_{0}^{t}{10cos(20\tau)(.01e^{-2500(t-\tau)}sin(998.7(t-\tau))d\tau}</math> |
|
|
|
|
|
<math>\Rightarrow i(t)=-.000014e^{-2500t}cos(998.7t)-.000034e^{-2500t}sin(998.7t)+.000014cos(20t)+.0000002sin(20t)</math> |
|
|
|
|
|
This doesn't look exactly like the answer we got above, but we expect this since convolution doesn't take initial conditions into account. |
|
|
|
|
|
===State Equations=== |
|
|
|
|
|
To begin the demonstration of a new method (state space equations), we want to translate the system into a set of state equations: |
|
|
|
|
|
<math>\begin{bmatrix} i \\ \dfrac{di}{dt} \end{bmatrix}=\begin{bmatrix} 0 & 1 \\ 1000000 & 10 \end{bmatrix} \begin{bmatrix} \int{idt} \\ i \end{bmatrix} + \begin{bmatrix} 0 \\ 100cos(20t) \end{bmatrix}</math> |
|
|
|
|
|
The initial conditions mean that |
|
|
|
|
|
<math> \int{idt}=\begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} \int{idt} \\ i \end{bmatrix} +0 </math> |
|
---- |
|
---- |
|
|
|
|
Laplace Transform Example: Series RLC Circuit
Problem
Given a series RLC circuit with  ,
,  , and
, and  , having power source
, having power source  , find an expression for
, find an expression for  if
if  and
and  .
.
Solution
We begin with the general formula for voltage drops around the circuit:

Substituting numbers, we get


Now, we take the Laplace Transform and get
![{\displaystyle {\dfrac {s}{s^{2}+20^{2}}}=I+0.01[sI-i(0)]+10000{\dfrac {I}{s}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d41d1c35be0a5e4fd3c631da2fa7024f9df58eac)
Using the fact that  , we get
, we get




Using partial fraction decomposition, we find that





Finally, we take the inverse Laplace transform to obtain

which is our answer.
Initial/Final Value Theorems
We now want to use the Initial and Final Value Theorems on this problem.
The Initial Value Theorem states that



In addition, when we actually evaluate  from our equation for
from our equation for  , we find it to be 0 as well. So, things check out there.
, we find it to be 0 as well. So, things check out there.
The Final Value Theorem states that



This time, when we actually evaluate i(∞) from the equation for  , we find it to be undefined. So here, the Final Value Theorem tells us something that is not necessarily true (in fact, because we have oscillating functions, we know that i(∞) will not be zero).
, we find it to be undefined. So here, the Final Value Theorem tells us something that is not necessarily true (in fact, because we have oscillating functions, we know that i(∞) will not be zero).
Bode Plot
To get a Bode plot, we use the transfer function:

We then use a program such as Octave or MATLAB to obtain the Bode plot, which looks like this:
Break Points
We can also use break points to approximate and/or validate the Bode plot.
The break points of our function are determined by the transfer function

The break points are:
 (40db/decade down)
(40db/decade down)
Looking at the top part of the Bode plot, we see that the graph is indeed going down at roughly 40db/decade at 1000.
Convolution
We now want to show how convolution can achieve the same result as our Laplace Transform methods.
Convolution means that

where  is the inverse Laplace transform of the transfer function.
is the inverse Laplace transform of the transfer function.
Here,

Thus,


This doesn't look exactly like the answer we got above, but we expect this since convolution doesn't take initial conditions into account.
State Equations
To begin the demonstration of a new method (state space equations), we want to translate the system into a set of state equations:

The initial conditions mean that

Written by Nathan Reeves ~ Checked by










![{\displaystyle {\dfrac {s}{s^{2}+20^{2}}}=I+0.01[sI-i(0)]+10000{\dfrac {I}{s}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d41d1c35be0a5e4fd3c631da2fa7024f9df58eac)