An Ideal Transformer Example

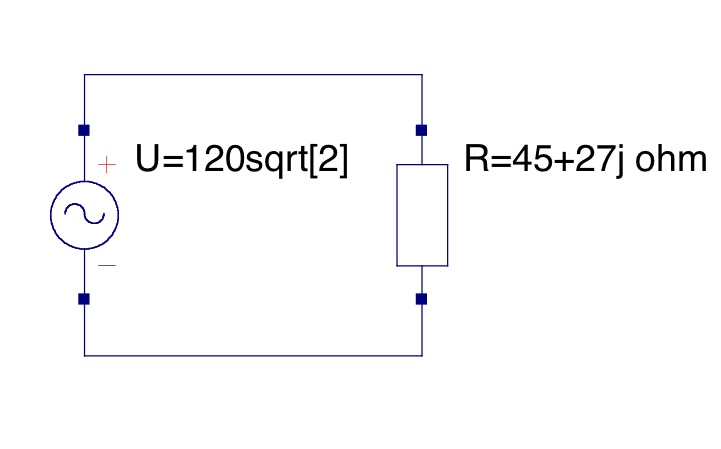
Consider a simple, transformer with two windings. Find the current provided by the voltage source.

• Winding 1 has a sinusoidal voltage of $120\sqrt{2}\mathrm{\angle }0$° applied to it at a frequency of 60Hz.
• $\frac{N_1}{N_2}=3$
• The combined load on winding 2 is ${Z}_L=(5+j3)\mathrm{\Omega }$

Solution

Given: ${e}_1(t)=V_1\cos (\omega t)$ and $\omega =2\pi f$

Substituting $f=60Hz$, $\omega =120\pi$

Therefore, ${e}_1(t)=120\sqrt{2}\cos (120\pi t)V$

Now the Thevenin equivalent impedance, ${Z}_{th}$, is found through the following steps:

$Z_{th}=\frac{e_1}{i_1}$

$=\frac{\frac{N_1}{N_2}{e}_2}{\frac{N_2}{N_1}{i}_2}$

$=(\frac{N_1}{N_2}{)}^2{R}_L$

Now, substituting:

${Z}_{th}=3^2(5+j3)$

$=(45+j27)\mathrm{\Omega }$

Since $i_1=\frac{e_1}{R_{th}}$,

$i_1=\frac{120\sqrt{2}}{45+j27}A$

Since this is an ideal transformer, it can be modeled by this simple circuit:

Contributors

Christopher Garrison Lau I

Reviwed By

Andrew Sell - Chris, everything looks fine, though I would do some extra formatting if possible to help make the problem flow a little smoother as you read it, and locate the picture a little higher to help bring the solution together.

Read By

John Hawkins