Using the Laplace Transform to solve a spring mass system that is critically damped
Problem Statement
An 8 pound weight is attached to a spring with a spring constant k of 4 lb/ft.
The spring is stretched 2 ft and rests at its equilibrium position.
It is then released from rest with an initial upward velocity of 3 ft/s.
The system contains a damping force of 2 times the initial velocity.
Solution
Things we know







Solving the problem






![{\displaystyle {\mathcal {L}}[{\frac {d^{2}x}{dt^{2}}}+8{\frac {dx}{dt}}+16x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9223069732914f355e25cc2ee4ac7c6e4b58e571)






![{\displaystyle {\mathcal {L}}^{-1}[-{\frac {3}{(s+4)^{2}}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dfc431d35b72b5580c7bbfb1bd441dfdfcb2394)



Apply the Initial and Final Value Theorems to find the initial and final values
- Initial Value Theorem

- Final Value Theorem

Applying this to our problem











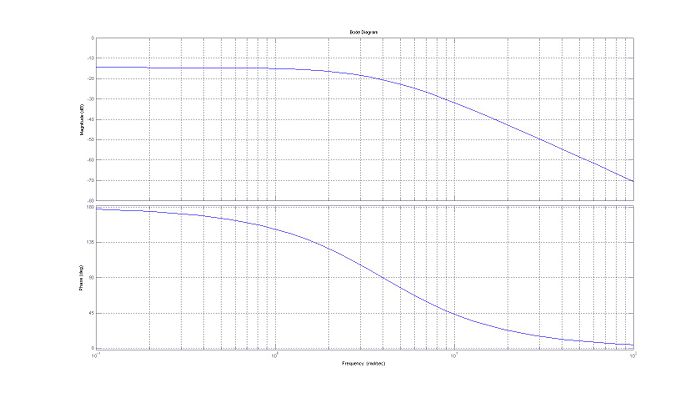
Bode Plot of the transfer function
Transfer Function

Bode Plot

==Break Points and Asymptotes==






Convolution











 ---
---
Written By: Mark Bernet
Error Checked By: Greg Peterson













![{\displaystyle {\mathcal {L}}[{\frac {d^{2}x}{dt^{2}}}+8{\frac {dx}{dt}}+16x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9223069732914f355e25cc2ee4ac7c6e4b58e571)






![{\displaystyle {\mathcal {L}}^{-1}[-{\frac {3}{(s+4)^{2}}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dfc431d35b72b5580c7bbfb1bd441dfdfcb2394)