09/29 - Analogy to Vector Spaces: Difference between revisions
Jump to navigation
Jump to search
| (5 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
**<math> a_1, a_2, a_3 \,\!</math> are the coefficients |
**<math> a_1, a_2, a_3 \,\!</math> are the coefficients |
||
**<math> \hat v_1, \hat v_2, \hat v_3 </math> are the basis vectors |
**<math> \hat v_1, \hat v_2, \hat v_3 </math> are the basis vectors |
||
**A vector basis is a set of n linearly independent vectors capable of |
**A vector basis is a set of n linearly independent vectors capable of generating an n-dimensional subspace of <math>\real^n</math> |
||
***Generating: using a linear combination of n vectors to be able to uniquely identify any part of the n-dimensional space |
|||
==Dot Product & Inner Product== |
==Dot Product & Inner Product== |
||
[[Image:300px-Dot_Product.svg.png|right|thumb|100px|Dot Product]] |
[[Image:300px-Dot_Product.svg.png|right|thumb|100px|Dot Product]] |
||
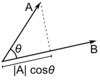
The dot (scalar) product takes two vectors over the real numbers and returns a real-valued scalar quantity. Geometrically, it will show the projection of one vector |
The dot (scalar) product takes two vectors over the real numbers and returns a real-valued scalar quantity. Geometrically, it will show the projection of one vector onto another. |
||
The dot product of two vectors <math> \ |
The dot product of two vectors <math> \vec a = {a_1, a_2, ..., a_n} \,\!</math> and <math> \vec b = {b_1, b_2, ..., b_n} \,\! </math> is defined as <math>\vec a \cdot \vec b = \sum_{i=1}^n a_i \cdot b_i = a_1b_1 + a_2b_2 + \cdots + a_nb_n </math> |
||
[[Image:783px-Inner-product-angle.png|right|thumb|100px|Inner Product]] |
[[Image:783px-Inner-product-angle.png|right|thumb|100px|Inner Product]] |
||
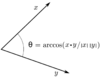
Since we will be dealing with complex numbers, we need to use the inner product instead of the dot product |
Since we will be dealing with complex numbers, we need to use the inner product instead of the dot product |
||
The inner product of two vectors <math> \ |
The inner product of two vectors <math> \vec a = {a_1 + b_1 j, a_2 + b_2 j, ... ,a_n + b_n j } </math> and <math> \vec b = {c_1 + d_1 j, c_2 + d_2 j, ... ,c_n + d_n j } </math> is defined as <math> \vec a \cdot \vec b = \sum_{i=1}^n a_i \cdot b_i^* </math> |
||
*Where <math> \ |
*Where <math> \vec b_i^* = {c_1 - d_1 j, c_2 - d_2 j, ... ,c_n - d_n j } </math> |
||
*Where is this info on Wikipedia? http://en.wikipedia.org/wiki/Inner_product_space |
*Where is this info on Wikipedia? http://en.wikipedia.org/wiki/Inner_product_space |
||
Latest revision as of 19:14, 11 November 2008
Analogy to Vector Spaces
Let the vector be defined as:
-
- are the coefficients
- are the basis vectors
- A vector basis is a set of n linearly independent vectors capable of generating an n-dimensional subspace of
- Generating: using a linear combination of n vectors to be able to uniquely identify any part of the n-dimensional space
Dot Product & Inner Product
The dot (scalar) product takes two vectors over the real numbers and returns a real-valued scalar quantity. Geometrically, it will show the projection of one vector onto another.
The dot product of two vectors and is defined as
Since we will be dealing with complex numbers, we need to use the inner product instead of the dot product
The inner product of two vectors and is defined as
- Where
- Where is this info on Wikipedia? http://en.wikipedia.org/wiki/Inner_product_space