09/29 - Analogy to Vector Spaces: Difference between revisions
Jump to navigation
Jump to search
| Line 11: | Line 11: | ||
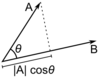
The dot (scalar) product takes two vectors over the real numbers and returns a real-valued scalar quantity. Geometrically, it will show the projection of one vector onto another. |
The dot (scalar) product takes two vectors over the real numbers and returns a real-valued scalar quantity. Geometrically, it will show the projection of one vector onto another. |
||
The dot product of two vectors <math> \ |
The dot product of two vectors <math> \vec a = {a_1, a_2, ..., a_n} \,\!</math> and <math> \vec b = {b_1, b_2, ..., b_n} \,\! </math> is defined as <math>\vec a \cdot \vec b = \sum_{i=1}^n a_i \cdot b_i = a_1b_1 + a_2b_2 + \cdots + a_nb_n </math> |
||
[[Image:783px-Inner-product-angle.png|right|thumb|100px|Inner Product]] |
[[Image:783px-Inner-product-angle.png|right|thumb|100px|Inner Product]] |
||
Since we will be dealing with complex numbers, we need to use the inner product instead of the dot product |
Since we will be dealing with complex numbers, we need to use the inner product instead of the dot product |
||
The inner product of two vectors <math> \ |
The inner product of two vectors <math> \vec a = {a_1 + b_1 j, a_2 + b_2 j, ... ,a_n + b_n j } </math> and <math> \vec b = {c_1 + d_1 j, c_2 + d_2 j, ... ,c_n + d_n j } </math> is defined as <math> \vec a \cdot \vec b = \sum_{i=1}^n a_i \cdot b_i^* </math> |
||
*Where <math> \ |
*Where <math> \vec b_i^* = {c_1 - d_1 j, c_2 - d_2 j, ... ,c_n - d_n j } </math> |
||
*Where is this info on Wikipedia? http://en.wikipedia.org/wiki/Inner_product_space |
*Where is this info on Wikipedia? http://en.wikipedia.org/wiki/Inner_product_space |
||
Revision as of 17:16, 10 November 2008
Analogy to Vector Spaces
Let the vector be defined as:
-
- are the coefficients
- are the basis vectors
- A vector basis is a set of n linearly independent vectors capable of generating an n-dimensional subspace of
- Generating: using a linear combination of n vectors to be able to uniquely identify any part of the n-dimensional space
Dot Product & Inner Product
The dot (scalar) product takes two vectors over the real numbers and returns a real-valued scalar quantity. Geometrically, it will show the projection of one vector onto another.
The dot product of two vectors and is defined as
Since we will be dealing with complex numbers, we need to use the inner product instead of the dot product
The inner product of two vectors and is defined as
- Where
- Where is this info on Wikipedia? http://en.wikipedia.org/wiki/Inner_product_space