|
|
| (8 intermediate revisions by the same user not shown) |
| Line 102: |
Line 102: |
|
:<math>\lambda_1=2.6626i\,</math> |
|
:<math>\lambda_1=2.6626i\,</math> |
|
:<math>\lambda_2=-2.6626i\,</math> |
|
:<math>\lambda_2=-2.6626i\,</math> |
|
:<math>\lambda_3=1.18766i\,</math> |
|
:<math>\lambda_3=1.1877i\,</math> |
|
:<math>\lambda_4=-1.18766i\,</math> |
|
:<math>\lambda_4=-1.1877i\,</math> |
|
|
|
|
|
== Eigen Vectors == |
|
== Eigen Vectors == |
| Line 138: |
Line 138: |
|
|
|
|
|
We can now plug these eigen vectors and eigen values into the standard equation |
|
We can now plug these eigen vectors and eigen values into the standard equation |
|
:<math>x=c_1k_1e^{\lambda_1 t}+c_2k_2e^{\lambda_2 t}+c_3k_3e^{\lambda_3 t}+c_4k_4e^{\lambda_4 t}</math> |
|
:<math>\bar{x}=c_1k_1e^{\lambda_1 t}+c_2k_2e^{\lambda_2 t}+c_3k_3e^{\lambda_3 t}+c_4k_4e^{\lambda_4 t}</math> |
|
|
|
|
|
And our final answer is |
|
And our final answer is |
|
:<math>x=c_1\begin{bmatrix} |
|
:<math>\bar{x}=c_1\begin{bmatrix} |
|
0.2149i \\ |
|
0.2149i \\ |
|
-0.5722 \\ |
|
-0.5722 \\ |
| Line 156: |
Line 156: |
|
-0.5407i \\ |
|
-0.5407i \\ |
|
0.6421 |
|
0.6421 |
|
\end{bmatrix}e^{1.18766it}+c_4\begin{bmatrix} |
|
\end{bmatrix}e^{1.1877it}+c_4\begin{bmatrix} |
|
0.3500i \\ |
|
0.3500i \\ |
|
0.4157 \\ |
|
0.4157 \\ |
|
0.5407i \\ |
|
0.5407i \\ |
|
0.6421 |
|
0.6421 |
|
\end{bmatrix}e^{-1.18766it}</math> |
|
\end{bmatrix}e^{-1.1877it}</math> |
|
|
|
|
|
|
|
|
== Matrix Exponential == |
|
== Matrix Exponential == |
|
|
We already know what the matrix A is from our state space equation |
|
In this section we will use matrix exponentials to solve the same problem. First we start with this identity. |
|
|
⚫ |
:<math>\bold{ A}=\begin{bmatrix} |
|
|
0 & 1 & 0 & 0 \\ |
|
|
-4.5 & 0 & 2 & 0 \\ |
|
|
0 & 0 & 0 & 1 \\ |
|
|
4 & 0 & -4 & 0 |
|
|
\end{bmatrix}</math> |
|
|
|
|
|
And we know that the T-inverse matrix is |
|
⚫ |
:<math>\ bold{ T^{-1}}=[\bar{ k_1} |\bar{k_2} |\ bar{ k_3} |\bar{ k_4} ]\,</math> |
|
⚫ |
:<math>\bold{T^{-1}}=\begin{bmatrix} |
|
|
0.2149i & -0.2149i & -0.3500i & 0.3500i \\ |
|
|
-0.5722 & -0.5722 & 0.4157 & 0.4157 \\ |
|
|
-0.2783i & 0.2783i & -0.5407i & 0.5407i \\ |
|
|
0.7409 & 0.7409 & 0.6421 & 0.6421 |
|
|
\end{bmatrix}</math> |
|
|
|
|
|
It then follows that matrix T is |
|
⚫ |
:<math>\bold{ T}=\begin{bmatrix} |
|
|
-1.2657i & -0.4753 & 0.8193i & 0.3077 \\ |
|
|
1.2657i & -0.4753 & -0.8193i & 0.3077 \\ |
|
|
0.6514i & 0.5484 & 0.5031i & 0.4236 \\ |
|
|
-0.6514i & 0.5484 & -0.5031 & 0.4236 |
|
|
\end{bmatrix}</math> |
|
|
|
|
|
Now we can use the equation for a transfer function to help us solve through the use of matrix exponentials. |
|
:<math>\bar{z}=\bold{T}\bar{x}\,</math> |
|
:<math>\bar{z}=\bold{T}\bar{x}\,</math> |
|
|
|
|
|
This can be rearranged by multiplying the inverse of '''T''' to the left side of the equation. |
|
This can be rearranged by multiplying '''T-inverse''' to the left side of the equations. |
|
:<math>\bold{T^{-1}}\bar{z}=\bar{x}\,</math> |
|
:<math>\bold{T^{-1}}\bar{z}=\bar{x}\,</math> |
|
|
|
|
|
Now we can use another identity that we already know |
|
Now we can bring in the standard form of a state space equation |
|
:<math>\dot{\bar{x}}=\bold{A}\bar{x}</math> |
|
:<math>\dot{\bar{x}}=\bold{A}\bar{x}</math> |
|
|
|
|
| Line 180: |
Line 204: |
|
:<math>\dot{\bar{z}}=\bold{TAT^{-1}}\bar{z}</math> |
|
:<math>\dot{\bar{z}}=\bold{TAT^{-1}}\bar{z}</math> |
|
:<math>\dot{\bar{z}}=\bold{\hat{A}}\bar{z}</math> |
|
:<math>\dot{\bar{z}}=\bold{\hat{A}}\bar{z}</math> |
|
|
|
|
This new equation has the same form as |
|
| ⚫ |
:<math>\ dot{\bar{ x}} =\ bold{ A}\bar{ x}</math> |
|
|
where |
|
where |
|
:<math>\bold{\hat{A}}=\bold{TAT^{-1}}</math> |
|
:<math>\bold{\hat{A}}=\bold{TAT^{-1}}</math> |
|
|
:<math>\bold{\hat{A}}= |
|
|
|
|
|
\begin{bmatrix} |
| ⚫ |
If we take the Laplace transform of this equation we can come up with the following |
|
|
|
-1.2657i & -0.4753 & 0.8193i & 0.3077 \\ |
| ⚫ |
:<math>\bar{ z}=e^{\bold{A}t}\bar{ z}(0)</math> |
|
|
|
1.2657i & -0.4753 & -0.8193i & 0.3077 \\ |
|
|
|
|
|
0.6514i & 0.5484 & 0.5031i & 0.4236 \\ |
|
If we calculate the value of <math>\bold{\hat{A}}</math> we will find that it is <math>\lambda\bold{I}</math> |
|
|
|
-0.6514i & 0.5484 & -0.5031 & 0.4236 |
| ⚫ |
:<math>\bold{ \hat{A}}=\begin{bmatrix} |
|
|
|
\end{bmatrix} |
|
|
\begin{bmatrix} |
|
|
0 & 1 & 0 & 0 \\ |
|
|
-{(k_1+k_2)\over {m_1}} & 0 & {k_2\over {m_1}} & 0 \\ |
|
|
0 & 0 & 0 & 1 \\ |
|
|
{k_2\over {m_2}} & 0 & -{k_2\over {m_2}} & 0 |
|
|
\end{bmatrix} |
|
|
\begin{bmatrix} |
|
|
0.2149i & -0.2149i & -0.3500i & 0.3500i \\ |
|
|
-0.5722 & -0.5722 & 0.4157 & 0.4157 \\ |
|
|
-0.2783i & 0.2783i & -0.5407i & 0.5407i \\ |
|
|
0.7409 & 0.7409 & 0.6421 & 0.6421 |
|
|
\end{bmatrix}</math> |
|
|
:<math>= |
|
|
\begin{bmatrix} |
|
2.6626i & 0 & 0 & 0 \\ |
|
2.6626i & 0 & 0 & 0 \\ |
|
0 & -2.6626i & 0 & 0 \\ |
|
0 & -2.6626i & 0 & 0 \\ |
| Line 198: |
Line 234: |
|
|
|
|
|
|
|
|
|
⚫ |
If we take the Laplace transform of the above equation we can come up with the following |
|
We also know what '''T''' equals and we can solve it for our case |
|
|
:<math>\bold{T^{-1}}=[\bar{k_1}|\bar{k_2}|\bar{k_3}|\bar{k_4}]\,</math> |
|
:<math>\bar{z}=e^{\bold{\hat{A}}t}\bar{z}(0)</math> |
|
|
where |
| ⚫ |
:<math>\bold{T^{-1}}=\begin{bmatrix} |
|
|
|
:<math>e^{\bold{\hat{A}}t}=\begin{bmatrix} |
|
|
e^{2.6626it} & 0 & 0 & 0 \\ |
|
|
0 & e^{-2.6626it} & 0 & 0 \\ |
|
|
0 & 0 & e^{1.1877it} & 0 \\ |
|
|
0 & 0 & 0 & e^{1.1877it} |
|
|
\end{bmatrix}</math> |
|
|
|
|
|
We then substitute this equation back into |
|
|
:<math>\bar{x}=\bold{T^{-1}}\bar{z}</math> |
|
|
and get |
|
|
:<math>\bar{x}=\bold{T^{-1}}e^{\bold{\hat{A}}t}\bar{z}(0)</math> |
|
|
:<math>\bar{x}=\bold{T^{-1}}e^{\bold{\hat{A}}t}\bold{T}\bar{x}(0)</math> |
|
|
Notice here that |
|
|
:<math>e^{\bold{A}t}=\bold{T^{-1}}e^{\bold{\hat{A}}t}\bold{T}</math> |
|
|
:<math>e^{\bold{A}t}=\begin{bmatrix} |
|
0.2149i & -0.2149i & -0.3500i & 0.3500i \\ |
|
0.2149i & -0.2149i & -0.3500i & 0.3500i \\ |
|
-0.5722 & -0.5722 & 0.4157 & 0.4157 \\ |
|
-0.5722 & -0.5722 & 0.4157 & 0.4157 \\ |
|
-0.2783i & 0.2783i & -0.5407i & 0.5407i \\ |
|
-0.2783i & 0.2783i & -0.5407i & 0.5407i \\ |
|
0.7409 & 0.7409 & 0.6421 & 0.6421 |
|
0.7409 & 0.7409 & 0.6421 & 0.6421 |
|
\end{bmatrix}</math> |
|
\end{bmatrix} |
|
|
\begin{bmatrix} |
|
|
|
|
|
e^{2.6626it} & 0 & 0 & 0 \\ |
|
Taking the inverse of this we can solve for '''T''' |
|
|
|
0 & e^{-2.6626it} & 0 & 0 \\ |
| ⚫ |
:<math>\bold{ T}=\begin{bmatrix} |
|
|
|
0 & 0 & e^{1.1877it} & 0 \\ |
|
|
0 & 0 & 0 & e^{1.1877it} |
|
|
\end{bmatrix} |
|
|
\begin{bmatrix} |
|
-1.2657i & -0.4753 & 0.8193i & 0.3077 \\ |
|
-1.2657i & -0.4753 & 0.8193i & 0.3077 \\ |
|
1.2657i & -0.4753 & -0.8193i & 0.3077 \\ |
|
1.2657i & -0.4753 & -0.8193i & 0.3077 \\ |
|
0.6514i & 0.5484 & 0.5031i & 0.4236 \\ |
|
0.6514i & 0.5484 & 0.5031i & 0.4236 \\ |
|
-0.6514i & 0.5484 & -0.5031 & 0.4236 |
|
-0.6514i & 0.5484 & -0.5031 & 0.4236 |
|
\end{bmatrix}</math> |
|
\end{bmatrix} |
|
|
</math> |
|
|
You can solve this with a computer program or your calculator and plug it into the equation for '''A'''. I have not listed the answer for this problem here because it is very messy and extremely long. I did calculate it to make sure it is solvable. But if your numbers are easier to work with you would finish by plugging this value into the equation below. |
|
⚫ |
:<math>\bar{ x}=e^{\bold{A}t}\bar{ x}(0)</math> |
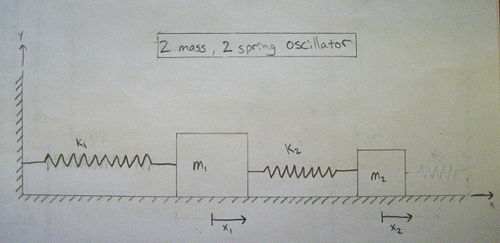
Problem
In this problem we will explore the solution of a double spring/mass system under the assumption that the blocks are resting on a smooth surface. Here's a picture of what we are working with.
Equations of Equilibrium
Using F=ma we can then find our four equations of equilibrium.
- Equation 1

- Equation 2

- Equation 3

- Equation 4

Now we can put these four equations into the state space form.

Eigen Values
Once you have your equations of equilibrium in matrix form you can plug them into a calculator or a computer program that will give you the eigen values automatically. This saves you a lot of hand work. Here's what you should come up with for this particular problem given these initial conditions.
- Given




We now have

From this we get




Eigen Vectors
Using the equation above and the same given conditions we can plug everything to a calculator or computer program like MATLAB and get the eigen vectors which we will denote as  .
.




Solving
We can now plug these eigen vectors and eigen values into the standard equation

And our final answer is

Matrix Exponential
We already know what the matrix A is from our state space equation

And we know that the T-inverse matrix is
![{\displaystyle {\mathbf {T^{-1}}}=[{\bar {k_{1}}}|{\bar {k_{2}}}|{\bar {k_{3}}}|{\bar {k_{4}}}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c521818ac2f043cfb41f9ef03c202704a3b8f8b)

It then follows that matrix T is

Now we can use the equation for a transfer function to help us solve through the use of matrix exponentials.

This can be rearranged by multiplying T-inverse to the left side of the equations.

Now we can bring in the standard form of a state space equation

Combining the two equations we then get

Multiplying both sides of the equation on the left by T we get


where



If we take the Laplace transform of the above equation we can come up with the following

where

We then substitute this equation back into

and get


Notice here that


You can solve this with a computer program or your calculator and plug it into the equation for A. I have not listed the answer for this problem here because it is very messy and extremely long. I did calculate it to make sure it is solvable. But if your numbers are easier to work with you would finish by plugging this value into the equation below.























![{\displaystyle {\mathbf {T^{-1}}}=[{\bar {k_{1}}}|{\bar {k_{2}}}|{\bar {k_{3}}}|{\bar {k_{4}}}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c521818ac2f043cfb41f9ef03c202704a3b8f8b)


















