DFT Developement (Brandon.Price)

The Fourier Transform is a powerful tool, but how can we use it with computers?

Let's take a look at the Fourier Transform and make some observations.

$X(f)={\mathcal {F}}(x(t))=\int _{-\infty }^{\infty }x(t)\ e^{-j2\pi tf}\,dt$

Here, we see an integration of time from negative infinity to infinity for the function $x(t)$. This is a problem for several reasons:

1)We have no access to data for a given function before we start observing (so we can't start at time = -infinity).

2) We can't wait until all time passes (ending at time = infinity) to compute the transform.

3) We can't use continuous integration since computers are restricted by finite memory.

We can get around each of these by noting that:

1) We don't care what happened to our signal before we started looking.

2) We don't care what happens to our signal after a certain (short) length of time.

3) we can approximate an integral using a summation (just like Riemann sums from the Calculus).

Our answer will not be the same as the true Fourier Transform, but as engineers, we are prepared to carefully sacrifice some precision for practicality. So, let's call this modification a "Discrete Fourier Transform (DFT)." How do we calculate one and how does it compare to the Fourier Transform?

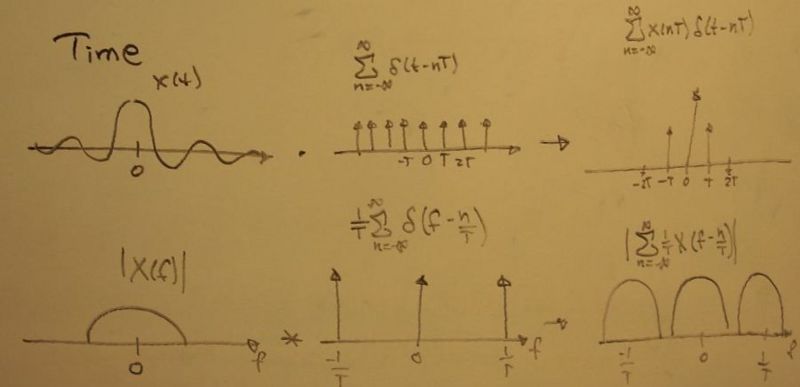
We start with an infinite continuous signal (in time) and multiply it by a sequence of delta functions, effectively sampling the continuous signal at discrete intervals. The resulting convolution in the frequency domain gives us a periodic frequency function.

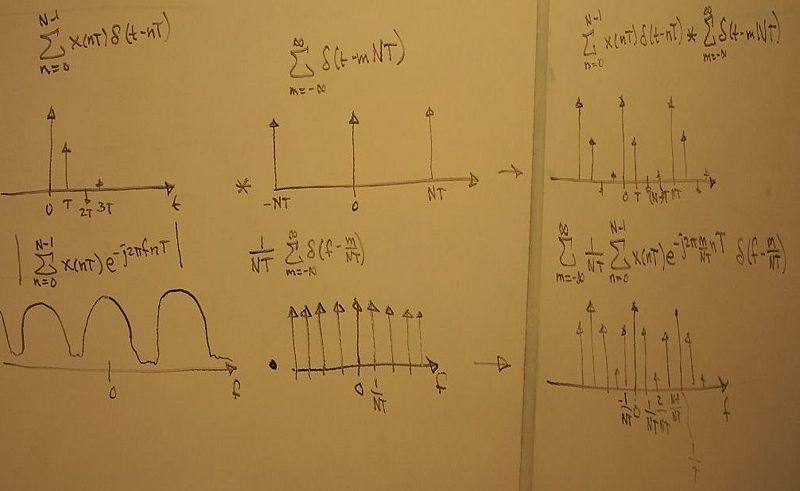
Next, we multiply our infinite series of impulse functions by a windowing function (this eliminates the data before and after the length of time we care about). Now we have a discrete representation (N samples) of just the part of the signal we want. In the frequency domain, we once again convolve, resulting in a slightly distorted, periodic frequency signal. (Fewer samples or smaller sample interval results in more distortion in the frequency domain).

We want to work with discrete frequency data too, in the computer, so we multiply the frequency domain by a sequence of impulse functions. The corresponding convolution in time makes our discrete sample periodic.

Now, we have a discrete representation of a small piece of the original continuous signal - both in time and frequency! Comparing the time domain and frequency domain, we can see the the DFT must be defined as:

$X(m)=DFT(x(nT))=\sum _{n=0}^{N-1}x(nT)\ e^{-j2\pi nm/N}$ for $m=0,\dots ,N-1$

Commonly, we write: x(nT) = x(n)

Let us reflect on these:

We notice that X(m) is periodic with period N since:

$X(m+N)=\sum _{n=0}^{N-1}x(nT)\ e^{-j2\pi n(m+N)/N}=\sum _{n=0}^{N-1}x(nT)\ e^{-j2\pi nm/N}e^{-j2\pi n}=\sum _{n=0}^{N-1}x(nT)\ e^{-j2\pi nm/N}=X(m)$

We also notice that with the following approximations, we can see a resemblance between the DFT and the Fourier Integral:

$f\approx {\frac {m}{NT}}$

$t\approx nT$

$\int dt\approx \sum T$

So, slipping these into the DFT and shifting our index by N/2 (since the sequence is periodic) we find:

$DFT(x(nT))=\sum _{n=0}^{N-1}x(nT)\ e^{\frac {-j2\pi nm}{N}}={\frac {1}{T}}\sum _{n=-N/2}^{N/2-1}x(nT)\ e^{-j2\pi nT({\frac {m}{NT}})}T\approx {\frac {1}{T}}\int _{-NT/2}^{NT/2}x(t)\ e^{-j2\pi tf}\,dt$

The only real differences are limits on the integral and the 1/T scaling factor. So, the DFT may not be such a bad approximation after all!