FIR Filter Example
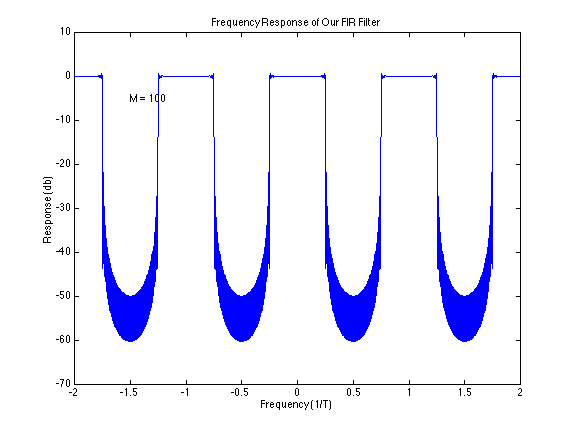
The filter coefficients are given by: where H(f) is the desired frequency response. See the notes from October 31, 2005. As an example of this filter we will make a Matlab script that will computer the frequency response for a low pass filter having a cutoff frequency of 1/(4T), and using 2M+1 coefficients. Note that it is periodic with period 1/T. This is the case with all digital filters.
Here is the plot the Matlab code produces:
The Matlab code to see the frequency response is given below:
% This shows how to find the frequency response for an FIR filter with cutoff 1/4/T and 2M+1 coefficients.
clf;
sum=0;
T=1;
fs=1/1000/T;
f=-2/T:fs:2/T
M=100;
for m=-M:M;
- if m==0
- h=1/2;
- else
- h=sin(pi*m/2)/(pi*m);
- end
- sum=sum+h*exp(-i*2*pi*f*m*T);
end
plot(f,20*log10(abs(sum)))
title('Frequency Response of Our FIR Filter')
xlabel('Frequency (1/T)')
ylabel('Response (db)')
text(-1.5,-5,'M = 100')
% End of Matlab code.