Gibbs Phenomenon: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
Michaelvier (talk | contribs) No edit summary |
||
| (4 intermediate revisions by one other user not shown) | |||
| Line 4: | Line 4: | ||
==The Phenomenon== |
==The Phenomenon== |
||
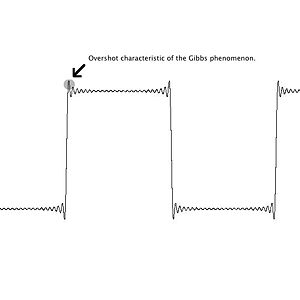
The identifying characteristic of the Gibbs phenomenon is the spike past where the Fourier series is summing to. As my colleagues previously stated, "notice how the summation function resembles the original periodic function more as more functions are added."<ref>[http://fweb/class-wiki/index.php/Fourier_Series:_Explained! Fourier Series: Explained!]</ref> |
The identifying characteristic of the Gibbs phenomenon is the spike past where the Fourier series is summing to. As my colleagues previously stated, "notice how the summation function resembles the original periodic function more as more functions are added."<ref>[http://fweb/class-wiki/index.php/Fourier_Series:_Explained! Fourier Series: Explained!]</ref> |
||
While this is true, it can also be seen that the jump does not diminish as the frequency of additional functions is increased. |
While this is true, it can also be seen that the jump does not diminish as the frequency of additional functions is increased. In fact the spike reaches a finite limit. |
||
[[Image:Gibbs_phenomenon_50.jpg|300px|thumb|right|Showing the spike at a discontinuity.]] |
[[Image:Gibbs_phenomenon_50.jpg|300px|thumb|right|Showing the spike at a discontinuity.]] |
||
==References== |
|||
<references/> |
|||
==Contributor== |
|||
*[[Grant, Joshua | Joshua Grant]] |
|||
===Reviewed By=== |
|||
*[[Vier, Michael | Michael Vier]] |
|||
===Read By=== |
|||
Latest revision as of 21:24, 18 January 2010
Overview
The Gibbs phenomenon is the the tendency for Fourier sums to "jump" higher than expected at discontinuities. It is named after the American physicist J. Willard Gibbs.
The Phenomenon
The identifying characteristic of the Gibbs phenomenon is the spike past where the Fourier series is summing to. As my colleagues previously stated, "notice how the summation function resembles the original periodic function more as more functions are added."<ref>Fourier Series: Explained!</ref> While this is true, it can also be seen that the jump does not diminish as the frequency of additional functions is increased. In fact the spike reaches a finite limit.
References
<references/>
Contributor