|
|
| Line 26: |
Line 26: |
|
|
|
|
|
<math>X_1(s)=\dfrac{m_1(sx_1(0)+\dot{x}_1(0))+k_2X_2(s)}{(m_1s^2+k_1+k_2)}</math> |
|
<math>X_1(s)=\dfrac{m_1(sx_1(0)+\dot{x}_1(0))+k_2X_2(s)}{(m_1s^2+k_1+k_2)}</math> |
|
|
|
|
|
<math>X_1(s)=\dfrac{1(s0+(-1)]+1X_2(s)}{(1s^2+1+1)}</math> |
|
|
|
|
|
<math>X_1(s)=\dfrac{X_2(s)-1}{(s^2+2)}</math> |
|
<math>X_1(s)=\dfrac{X_2(s)-1}{(s^2+2)}</math> |
| Line 37: |
Line 39: |
|
|
|
|
|
<math>X_2(s)=\dfrac{m_2(sx_2(0)+\dot{x}_2(0))+k_2X_1(s)}{(m_2s^2+k_2+k_3)}</math> |
|
<math>X_2(s)=\dfrac{m_2(sx_2(0)+\dot{x}_2(0))+k_2X_1(s)}{(m_2s^2+k_2+k_3)}</math> |
|
|
|
|
|
<math>X_2(s)=\dfrac{1(s0+1)+1X_1(s)}{(1s^2+1+1)}</math> |
|
|
|
|
|
<math>X_2(s)=\dfrac{X_1(s)+1}{(s^2+2)}</math> |
|
<math>X_2(s)=\dfrac{X_1(s)+1}{(s^2+2)}</math> |
Revision as of 14:57, 23 November 2009
Problem Statement
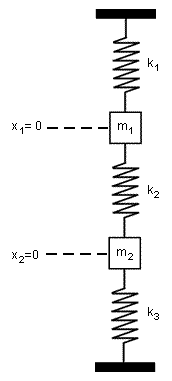
Figure 1. Coupled Spring System.
Derive the system of differential equations describing the straight-line vertical motion of the coupled spring shown in Figure 1. Use Laplace transform to solve the system when  ,
,  , and
, and  ,
,  ,
,  , and
, and  .
.
Solution
At positions  and
and  , the masses
, the masses  and
and  are in equilibrium. Thus, the motion equations for
are in equilibrium. Thus, the motion equations for  and
and  are,
are,
 ∴
∴ 
 ∴
∴ 
where  and
and  represent the Newton's Second Law of Motion and
represent the Newton's Second Law of Motion and  and
and  represent the net forces acting in the masses.
represent the net forces acting in the masses.
Laplace Transform
Applying the Laplace Transform to the motion equations and plugging the values of  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  for this systems, we obtain,
for this systems, we obtain,
![{\displaystyle {\mathcal {L}}[m_{1}{\ddot {x}}_{1}+k_{1}x_{1}-k_{2}(x_{2}-x_{1})]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e19d54f8103862c365531abd9d680e30699921bd)
![{\displaystyle m_{1}[s^{2}X_{1}(s)-sx_{1}(0)-{\dot {x}}_{1}(0)]+k_{1}X_{1}(s)-k_{2}(X_{2}(s)-X_{1}(s))=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1deac8eae96cf41b770d2c0e1b1c6d4bf8c56a66)


![{\displaystyle X_{1}(s)={\dfrac {1(s0+(-1)]+1X_{2}(s)}{(1s^{2}+1+1)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1569d4323a471f35f58c9deed7a415e1d26dfdea)

![{\displaystyle {\mathcal {L}}[m_{2}{\ddot {x}}_{2}+k_{2}(x_{2}-x_{1})+k_{3}x_{2}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4707b281c937d686208365d5f59b7edb113f358c)
![{\displaystyle m_{2}[s^{2}X_{2}(s)-sx_{2}(0)-{\dot {x}}_{2}(0)]+k_{2}(X_{2}(s)-X_{1}(s))+k_{3}X_{2}(s)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13011c53d33b219ef915a9baa26cb6667a8c8529)




Finally, solving for  and
and  yields,
yields,


Inverse Laplace Transform
First, we recognize that

On the other hand, we identify that  , and so
, and so  . Hence, we fix the expression by multiplying and dividing by
. Hence, we fix the expression by multiplying and dividing by  ,
,
![{\displaystyle {\mathcal {L}}^{-1}[X_{1}(s)]={\mathcal {L}}^{-1}\left[{\dfrac {-1}{s^{2}+3}}\right]=-{\dfrac {1}{\sqrt {3}}}{\mathcal {L}}^{-1}\left[{\dfrac {\sqrt {3}}{s^{2}+3}}\right]=-{\dfrac {1}{\sqrt {3}}}sin({\sqrt {3}}t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5614cea3dad45c4ccf8dc14e16647cb1165eb175)
![{\displaystyle {\mathcal {L}}^{-1}[X_{2}(s)]={\mathcal {L}}^{-1}\left[{\dfrac {1}{s^{2}+3}}\right]={\dfrac {1}{\sqrt {3}}}{\mathcal {L}}^{-1}\left[{\dfrac {\sqrt {3}}{s^{2}+3}}\right]={\dfrac {1}{\sqrt {3}}}sin({\sqrt {3}}t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/832c950870d8129efb0fc7a4dd8d6464872b963b)


























![{\displaystyle {\mathcal {L}}[m_{1}{\ddot {x}}_{1}+k_{1}x_{1}-k_{2}(x_{2}-x_{1})]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e19d54f8103862c365531abd9d680e30699921bd)
![{\displaystyle m_{1}[s^{2}X_{1}(s)-sx_{1}(0)-{\dot {x}}_{1}(0)]+k_{1}X_{1}(s)-k_{2}(X_{2}(s)-X_{1}(s))=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1deac8eae96cf41b770d2c0e1b1c6d4bf8c56a66)


![{\displaystyle X_{1}(s)={\dfrac {1(s0+(-1)]+1X_{2}(s)}{(1s^{2}+1+1)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1569d4323a471f35f58c9deed7a415e1d26dfdea)

![{\displaystyle {\mathcal {L}}[m_{2}{\ddot {x}}_{2}+k_{2}(x_{2}-x_{1})+k_{3}x_{2}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4707b281c937d686208365d5f59b7edb113f358c)
![{\displaystyle m_{2}[s^{2}X_{2}(s)-sx_{2}(0)-{\dot {x}}_{2}(0)]+k_{2}(X_{2}(s)-X_{1}(s))+k_{3}X_{2}(s)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13011c53d33b219ef915a9baa26cb6667a8c8529)












![{\displaystyle {\mathcal {L}}^{-1}[X_{1}(s)]={\mathcal {L}}^{-1}\left[{\dfrac {-1}{s^{2}+3}}\right]=-{\dfrac {1}{\sqrt {3}}}{\mathcal {L}}^{-1}\left[{\dfrac {\sqrt {3}}{s^{2}+3}}\right]=-{\dfrac {1}{\sqrt {3}}}sin({\sqrt {3}}t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5614cea3dad45c4ccf8dc14e16647cb1165eb175)
![{\displaystyle {\mathcal {L}}^{-1}[X_{2}(s)]={\mathcal {L}}^{-1}\left[{\dfrac {1}{s^{2}+3}}\right]={\dfrac {1}{\sqrt {3}}}{\mathcal {L}}^{-1}\left[{\dfrac {\sqrt {3}}{s^{2}+3}}\right]={\dfrac {1}{\sqrt {3}}}sin({\sqrt {3}}t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/832c950870d8129efb0fc7a4dd8d6464872b963b)