|
|
| Line 1: |
Line 1: |
|
__TOC__ |
|
__TOC__ |
|
|
|
|
|
|
[[Image:Figure1.gif|thumb|Figure 1. Coupled Spring System.]] |
|
= Problem Statement = |
|
= Problem Statement = |
|
[[Image:Figure1.gif|thumb|Figure 1. Coupled Spring System.]]Derive the system of differential equations describing the straight-line vertical motion of the coupled spring shown in Figure 1. Use Laplace transform to solve the system when <math>k_1=k_2=k_3=1</math>, <math>m_1=m_2=1</math>, and <math>x_1(0)=0</math>, <math>x'1(0)=-1</math>, <math>x_2(0)=0</math>, and <math>x'_2(0)=1</math>.
|
|
Derive the system of differential equations describing the straight-line vertical motion of the coupled spring shown in Figure 1. Use Laplace transform to solve the system when <math>k_1=k_2=k_3=1</math>, <math>m_1=m_2=1</math>, and <math>x_1(0)=0</math>, <math>x'1(0)=-1</math>, <math>x_2(0)=0</math>, and <math>x'_2(0)=1</math>. |
|
|
|
|
|
= Solution = |
|
= Solution = |
|
At positions <math>x_1</math> and <math>x_2</math>, the masses <math>m_1</math> and <math>m_2</math> are in equilibrium. Thus, the motion equations for <math>m_1</math> and <math>m_2</math> are, |
|
At positions <math>x_1</math> and <math>x_2</math>, the masses <math>m_1</math> and <math>m_2</math> are in equilibrium. Thus, the motion equations for <math>m_1</math> and <math>m_2</math> are, |
|
|
|
|
|
<math>m_1\ddot{x}_1=-k_1x_1+k_2(x_2-x_1)</math>
|
|
:<math>m_1\ddot{x}_1=-k_1x_1+k_2(x_2-x_1)</math> |
|
∴ <math>m_1\ddot{x}_1+k_1x_1-k_2(x_2-x_1)=0</math>
|
|
:∴<math>m_1\ddot{x}_1+k_1x_1-k_2(x_2-x_1)=0</math> |
|
|
|
|
|
<math>m_2\ddot{x}_2=-k_2(x_2-x_1)-k_3x_2</math>
|
|
:<math>m_2\ddot{x}_2=-k_2(x_2-x_1)-k_3x_2</math> |
|
∴ <math>m_2\ddot{x}_2+k_2(x_2-x_1)-k_3x_2=0</math>
|
|
:∴ <math>m_2\ddot{x}_2+k_2(x_2-x_1)-k_3x_2=0</math> |
|
|
|
|
|
|
|
|
| Line 19: |
Line 20: |
|
Applying the Laplace Transform to the motion equations and plugging the values of <math>k_1</math>, <math>k_2</math>, <math>k_3</math>, <math>m_1</math>, <math>m_2</math>, <math>x_1(0)</math>, <math>x'1(0)</math>, <math>x_2(0)</math>, and <math>x'_2(0)</math> for this systems, we obtain, |
|
Applying the Laplace Transform to the motion equations and plugging the values of <math>k_1</math>, <math>k_2</math>, <math>k_3</math>, <math>m_1</math>, <math>m_2</math>, <math>x_1(0)</math>, <math>x'1(0)</math>, <math>x_2(0)</math>, and <math>x'_2(0)</math> for this systems, we obtain, |
|
|
|
|
|
<math>\mathcal{L}[m_1\ddot{x}_1+k_1x_1-k_2(x_2-x_1)]=0</math>
|
|
:<math>\mathcal{L}[m_1\ddot{x}_1+k_1x_1-k_2(x_2-x_1)]=0</math> |
|
⚫ |
::<math> m_1[s^ 2X_1(s)- sx_1(0)-\dot{x} _1(0)]+ k_1X_1(s)-k_2(X_2(s)-X_1(s))=0</math> |
|
⚫ |
::<math> X_1(s)( m_1s^2+ k_1+ k_2)= m_1( sx_1(0)-\dot{x} _1(0))+ k_2X_2(s)</math> |
|
⚫ |
::<math> X_1(s)=\dfrac{ m_1( sx_1(0)+\dot{x} _1(0))+ k_2X_2(s)}{( m_1s^2+ k_1+ k_2)}</math> |
|
⚫ |
::<math>X_1(s)=\dfrac{1(s0+(-1)]+1X_2(s)}{(1s^2+1+1)}</math> |
|
⚫ |
::<math>X_1(s)=\dfrac{X_2(s)-1}{(s^2+2)}</math> |
|
|
|
|
|
<math>m_1[s^2X_1(s)-sx_1(0)-\dot{x}_1(0)]+k_1X_1(s)-k_2(X_2(s)-X_1(s))=0</math>
|
|
:<math>\mathcal{L}[m_2\ddot{x}_2+k_2(x_2-x_1)+k_3x_2]=0</math> |
|
|
::<math>m_2[s^2X_2(s)-sx_2(0)-\dot{x}_2(0)]+k_2(X_2(s)-X_1(s))+k_3X_2(s)=0</math> |
|
|
|
|
<math>X_1(s)(m_1s^2+k_1+k_2)=m_1(sx_1(0)-\dot{x}_1(0))+k_2X_2(s)</math>
|
|
::<math>X_2(s)(m_2s^2+k_2+k_3)=m_2(sx_2(0)-\dot{x}_2(0))+k_2X_1(s)</math> |
|
⚫ |
::<math>X_2(s)=\dfrac{ m_2( sx_2(0)+ \dot{x}_2(0))+ k_2X_1(s)}{( m_2s^2+ k_2+ k_3)}</math> |
|
|
|
|
<math>X_1(s)=\dfrac{m_1(sx_1(0)+\dot{x}_1(0))+k_2X_2(s)}{(m_1s^2+k_1+k_2)}</math>
|
|
::<math>X_2(s)=\dfrac{1(s0+1)+1X_1(s)}{(1s^2+1+1)}</math> |
|
⚫ |
::<math>X_2(s)=\dfrac{X_1(s)+1}{(s^2+2)}</math> |
|
|
|
| ⚫ |
<math>X_1(s)=\dfrac{1(s0+(-1)]+1X_2(s)}{(1s^2+1+1)}</math> |
|
|
|
|
| ⚫ |
<math>X_1(s)=\dfrac{X_2(s)-1}{(s^2+2)}</math> |
|
|
|
|
|
|
|
|
<math>\mathcal{L}[m_2\ddot{x}_2+k_2(x_2-x_1)+k_3x_2]=0</math> |
|
|
|
|
| ⚫ |
<math> m_2[s^ 2X_2(s)- sx_2(0)-\dot{x} _2(0)]+k_2(X_2(s)-X_1(s) )+k_3X_2(s)=0</math> |
|
|
|
|
| ⚫ |
<math> X_2(s)( m_2s^2+ k_2+ k_3)= m_2( sx_2(0)-\dot{x} _2(0))+ k_2X_1(s)</math> |
|
|
|
|
| ⚫ |
<math> X_2(s)=\dfrac{ m_2( sx_2(0)+\dot{x} _2(0))+ k_2X_1(s)}{( m_2s^2+ k_2+ k_3)}</math> |
|
|
|
|
| ⚫ |
<math>X_2(s)=\dfrac{ 1( s0+ 1)+ 1X_1(s)}{( 1s^2+ 1+ 1)}</math> |
|
|
|
|
| ⚫ |
<math>X_2(s)=\dfrac{X_1(s)+1}{(s^2+2)}</math> |
|
|
|
|
|
|
Finally, solving for <math>X_1(s)</math> and <math>X_2(s)</math> yields, |
|
Finally, solving for <math>X_1(s)</math> and <math>X_2(s)</math> yields, |
|
|
|
|
|
<math>X_1(s)=\dfrac{-1}{s^2+3}</math>
|
|
:<math>X_1(s)=\dfrac{-1}{s^2+3}</math> |
|
⚫ |
:<math>X_2(s)=\dfrac{1}{s^2+3}</math> |
|
|
|
|
|
|
| ⚫ |
<math>X_2(s)=\dfrac{1}{s^2+3}</math> |
|
|
|
|
|
|
== Inverse Laplace Transform == |
|
== Inverse Laplace Transform == |
|
|
[[Image:mass_spring_displacement_plot.png|thumb|Figure 2. Coupled Spring System Displacement.]] |
|
|
|
|
First, we recognize that |
|
First, we recognize that |
|
|
|
|
| Line 58: |
Line 48: |
|
On the other hand, we identify that <math>k^2=3</math>, and so <math>k=\sqrt{3}</math>. Hence, we fix the expression by multiplying and dividing by <math>\sqrt{3}</math>, |
|
On the other hand, we identify that <math>k^2=3</math>, and so <math>k=\sqrt{3}</math>. Hence, we fix the expression by multiplying and dividing by <math>\sqrt{3}</math>, |
|
|
|
|
|
<math>\mathcal{L}^{-1}[X_1(s)] = \mathcal{L}^{-1} \left [ \dfrac{-1}{s^2+3} \right ] = -\dfrac{1}{\sqrt{3}} \mathcal{L}^{-1} \left [ \dfrac{\sqrt{3}}{s^2+3} \right ] = -\dfrac{1}{\sqrt{3}} sin(\sqrt{3}t)</math>
|
|
:<math>x_1(t)=\mathcal{L}^{-1}[X_1(s)] = \mathcal{L}^{-1} \left [ \dfrac{-1}{s^2+3} \right ] = -\dfrac{1}{\sqrt{3}} \mathcal{L}^{-1} \left [ \dfrac{\sqrt{3}}{s^2+3} \right ] = -\dfrac{1}{\sqrt{3}} sin(\sqrt{3}t)</math> |
|
|
|
|
|
|
|
<math>\mathcal{L}^{-1}[X_2(s)] = \mathcal{L}^{-1} \left [ \dfrac{1}{s^2+3} \right ] = \dfrac{1}{\sqrt{3}} \mathcal{L}^{-1} \left [ \dfrac{\sqrt{3}}{s^2+3} \right ] = \dfrac{1}{\sqrt{3}} sin(\sqrt{3}t)</math>
|
|
:<math>x_2=(t)\mathcal{L}^{-1}[X_2(s)] = \mathcal{L}^{-1} \left [ \dfrac{1}{s^2+3} \right ] = \dfrac{1}{\sqrt{3}} \mathcal{L}^{-1} \left [ \dfrac{\sqrt{3}}{s^2+3} \right ] = \dfrac{1}{\sqrt{3}} sin(\sqrt{3}t)</math> |
|
|
|
|
|
A plot of the system displacement is shown on Figure 2. |
|
A plot of the system displacement is shown on Figure 2. |
|
|
|
|
|
|
|
|
== Initial-Value & Final-Value Theorem == |
|
== Initial-Value & Final-Value Theorem == |
| Line 76: |
Line 67: |
|
Thus, applying both theorems to our the Laplace Transforms, |
|
Thus, applying both theorems to our the Laplace Transforms, |
|
|
|
|
|
<math>\lim_{s\rightarrow \infty} sX_1(s)=\lim_{s\rightarrow \infty} s\dfrac{-1}{s^2+3}=\lim_{s\rightarrow \infty} \dfrac{-s}{s^2+3}=\dfrac{-\infty}{\infty^2+3}=0=x_1(0)\,</math>
|
|
:<math>\lim_{s\rightarrow \infty} sX_1(s)=\lim_{s\rightarrow \infty} s\dfrac{-1}{s^2+3}=\lim_{s\rightarrow \infty} \dfrac{-s}{s^2+3}=\dfrac{-\infty}{\infty^2+3}=0=x_1(0)\,</math> |
|
⚫ |
:<math>\lim_{s\rightarrow 0} sX_1(s)==\lim_{s\rightarrow 0} s\dfrac{1}{s^2+3}=\lim_{s\rightarrow 0} \dfrac{s}{s^2+3}=\dfrac{0}{0^2+3}=0=x_1(\infty)\,</math> |
|
|
|
|
|
|
| ⚫ |
<math>\lim_{s\rightarrow \infty} sX_2(s)=\lim_{s\rightarrow \infty} s\dfrac{1}{s^2+3}=\lim_{s\rightarrow \infty} \dfrac{s}{s^2+3}=\dfrac{\infty}{\infty^2+3}=0=x_2(0)\,</math> |
|
|
|
|
|
⚫ |
:<math>\lim_{s\rightarrow \infty} sX_2(s)=\lim_{s\rightarrow \infty} s\dfrac{1}{s^2+3}=\lim_{s\rightarrow \infty} \dfrac{s}{s^2+3}=\dfrac{\infty}{\infty^2+3}=0=x_2(0)\,</math> |
|
⚫ |
:<math>\lim_{s\rightarrow 0} sX_2(s)==\lim_{s\rightarrow 0} s\dfrac{1}{s^2+3}=\lim_{s\rightarrow 0} \dfrac{s}{s^2+3}=\dfrac{0}{0^2+3}=0=x_2(\infty)\,</math> |
|
|
|
|
| ⚫ |
<math>\lim_{s\rightarrow 0} sX_1(s)==\lim_{s\rightarrow 0} s\dfrac{1}{s^2+3}=\lim_{s\rightarrow 0} \dfrac{s}{s^2+3}=\dfrac{0}{0^2+3}=0=x_1(\infty)\,</math> |
|
|
|
|
| ⚫ |
<math>\lim_{s\rightarrow 0} sX_2(s)==\lim_{s\rightarrow 0} s\dfrac{1}{s^2+3}=\lim_{s\rightarrow 0} \dfrac{s}{s^2+3}=\dfrac{0}{0^2+3}=0=x_2(\infty)\,</math> |
|
|
|
|
|
|
== Bode Plot == |
|
== Bode Plot == |
|
|
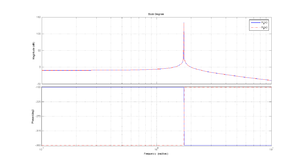
[[Image:Mass_spring_bode_plot.png|thumb|Figure 3. Bode Diagram.]]The Bode plot can be easily done using a program like Octave or MATLAB. The code is displayed below. From Figure 3 we may notice that the Amplitude vs. Frequency plot for both functions overlaps. On the other hand, the Phase vs. Frequency plot for both functions have opossite magnitudesNotice that both functions overlaps. |
|
The Bode plot can be easily done using a program like Octave or MATLAB. |
|
|
|
|
|
|
h1=tf([-1],[1 0 3]); |
|
|
h2=tf([1],[1 0 3]); |
|
|
bode(h1,'b',h2,'r'); |
|
|
|
|
|
== Magnitude Frequency Response == |
|
== Magnitude Frequency Response == |
| Line 92: |
Line 87: |
|
|
|
|
|
== State Equation Model == |
|
== State Equation Model == |
|
|
|
|
|
= References = |
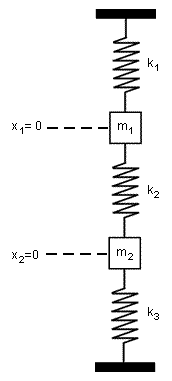
Figure 1. Coupled Spring System.
Problem Statement
Derive the system of differential equations describing the straight-line vertical motion of the coupled spring shown in Figure 1. Use Laplace transform to solve the system when  ,
,  , and
, and  ,
,  ,
,  , and
, and  .
.
Solution
At positions  and
and  , the masses
, the masses  and
and  are in equilibrium. Thus, the motion equations for
are in equilibrium. Thus, the motion equations for  and
and  are,
are,

- ∴


- ∴

where  and
and  represent the Newton's Second Law of Motion and
represent the Newton's Second Law of Motion and  and
and  represent the net forces acting in the masses.
represent the net forces acting in the masses.
Laplace Transform
Applying the Laplace Transform to the motion equations and plugging the values of  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  for this systems, we obtain,
for this systems, we obtain,
![{\displaystyle {\mathcal {L}}[m_{1}{\ddot {x}}_{1}+k_{1}x_{1}-k_{2}(x_{2}-x_{1})]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e19d54f8103862c365531abd9d680e30699921bd)
![{\displaystyle m_{1}[s^{2}X_{1}(s)-sx_{1}(0)-{\dot {x}}_{1}(0)]+k_{1}X_{1}(s)-k_{2}(X_{2}(s)-X_{1}(s))=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1deac8eae96cf41b770d2c0e1b1c6d4bf8c56a66)


![{\displaystyle X_{1}(s)={\dfrac {1(s0+(-1)]+1X_{2}(s)}{(1s^{2}+1+1)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1569d4323a471f35f58c9deed7a415e1d26dfdea)

![{\displaystyle {\mathcal {L}}[m_{2}{\ddot {x}}_{2}+k_{2}(x_{2}-x_{1})+k_{3}x_{2}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4707b281c937d686208365d5f59b7edb113f358c)
![{\displaystyle m_{2}[s^{2}X_{2}(s)-sx_{2}(0)-{\dot {x}}_{2}(0)]+k_{2}(X_{2}(s)-X_{1}(s))+k_{3}X_{2}(s)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13011c53d33b219ef915a9baa26cb6667a8c8529)




Finally, solving for  and
and  yields,
yields,


Inverse Laplace Transform
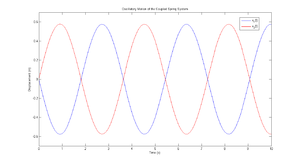
Figure 2. Coupled Spring System Displacement.
First, we recognize that

On the other hand, we identify that  , and so
, and so  . Hence, we fix the expression by multiplying and dividing by
. Hence, we fix the expression by multiplying and dividing by  ,
,
![{\displaystyle x_{1}(t)={\mathcal {L}}^{-1}[X_{1}(s)]={\mathcal {L}}^{-1}\left[{\dfrac {-1}{s^{2}+3}}\right]=-{\dfrac {1}{\sqrt {3}}}{\mathcal {L}}^{-1}\left[{\dfrac {\sqrt {3}}{s^{2}+3}}\right]=-{\dfrac {1}{\sqrt {3}}}sin({\sqrt {3}}t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a32d68f215f452efdbcce10a11e1b233a8fc230)
![{\displaystyle x_{2}=(t){\mathcal {L}}^{-1}[X_{2}(s)]={\mathcal {L}}^{-1}\left[{\dfrac {1}{s^{2}+3}}\right]={\dfrac {1}{\sqrt {3}}}{\mathcal {L}}^{-1}\left[{\dfrac {\sqrt {3}}{s^{2}+3}}\right]={\dfrac {1}{\sqrt {3}}}sin({\sqrt {3}}t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19364b5f445eb5a82d33a1d0b3ae49ec90388a72)
A plot of the system displacement is shown on Figure 2.
Initial-Value & Final-Value Theorem
The initial-value and final-value theorem can be useful the finding the behavior of a functionat small and large times respectively. By definition, the Initial-Value Theorem is,

and the Final-Value Theorem is,

Thus, applying both theorems to our the Laplace Transforms,




Bode Plot
The Bode plot can be easily done using a program like Octave or MATLAB. The code is displayed below. From Figure 3 we may notice that the Amplitude vs. Frequency plot for both functions overlaps. On the other hand, the Phase vs. Frequency plot for both functions have opossite magnitudesNotice that both functions overlaps.
h1=tf([-1],[1 0 3]);
h2=tf([1],[1 0 3]);
bode(h1,'b',h2,'r');
Magnitude Frequency Response
Convolution
State Equation Model
References


























![{\displaystyle {\mathcal {L}}[m_{1}{\ddot {x}}_{1}+k_{1}x_{1}-k_{2}(x_{2}-x_{1})]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e19d54f8103862c365531abd9d680e30699921bd)
![{\displaystyle m_{1}[s^{2}X_{1}(s)-sx_{1}(0)-{\dot {x}}_{1}(0)]+k_{1}X_{1}(s)-k_{2}(X_{2}(s)-X_{1}(s))=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1deac8eae96cf41b770d2c0e1b1c6d4bf8c56a66)


![{\displaystyle X_{1}(s)={\dfrac {1(s0+(-1)]+1X_{2}(s)}{(1s^{2}+1+1)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1569d4323a471f35f58c9deed7a415e1d26dfdea)

![{\displaystyle {\mathcal {L}}[m_{2}{\ddot {x}}_{2}+k_{2}(x_{2}-x_{1})+k_{3}x_{2}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4707b281c937d686208365d5f59b7edb113f358c)
![{\displaystyle m_{2}[s^{2}X_{2}(s)-sx_{2}(0)-{\dot {x}}_{2}(0)]+k_{2}(X_{2}(s)-X_{1}(s))+k_{3}X_{2}(s)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13011c53d33b219ef915a9baa26cb6667a8c8529)













![{\displaystyle x_{1}(t)={\mathcal {L}}^{-1}[X_{1}(s)]={\mathcal {L}}^{-1}\left[{\dfrac {-1}{s^{2}+3}}\right]=-{\dfrac {1}{\sqrt {3}}}{\mathcal {L}}^{-1}\left[{\dfrac {\sqrt {3}}{s^{2}+3}}\right]=-{\dfrac {1}{\sqrt {3}}}sin({\sqrt {3}}t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a32d68f215f452efdbcce10a11e1b233a8fc230)
![{\displaystyle x_{2}=(t){\mathcal {L}}^{-1}[X_{2}(s)]={\mathcal {L}}^{-1}\left[{\dfrac {1}{s^{2}+3}}\right]={\dfrac {1}{\sqrt {3}}}{\mathcal {L}}^{-1}\left[{\dfrac {\sqrt {3}}{s^{2}+3}}\right]={\dfrac {1}{\sqrt {3}}}sin({\sqrt {3}}t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19364b5f445eb5a82d33a1d0b3ae49ec90388a72)