Laplace transforms: Simple Electrical Network: Difference between revisions
Jump to navigation
Jump to search
| (22 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
<math>RC\dfrac{di_R}{dt}+i_R-i_C=0</math> |
<math>RC\dfrac{di_R}{dt}+i_R-i_C=0</math> |
||
Solve the system when V0 = 50 V, L = |
Solve the system when V0 = 50 V, L = 4 h, R = 20 Ω, C = 10<sup>-4</sup> f, and the currents are initially zero. |
||
==Solution== |
==Solution== |
||
Solve the system when V0 = 50 V, L = |
Solve the system when V0 = 50 V, L = 4 h, R = 20 Ω, C = 10<sup>-4</sup> f, and the currents are initially zero. |
||
Substituting numbers into the equations, we have |
|||
<math> |
<math>4\frac{di_1}{dt}+20i_2=50</math> |
||
<math> |
<math>20(10^{-4})\frac{di_2}{dt}+i_2-i_1=0</math> |
||
Applying the Laplace transform to each equation gives |
Applying the Laplace transform to each equation gives |
||
<math> |
<math>4(s\mathcal{L}\left\{i_1\right\}-i_1(0))+20\mathcal{L}\left\{i_2\right\}=50</math> |
||
<math></math> |
<math>\Rightarrow4sI_1(s)+20I_2(s)=\frac{50}{s}</math> |
||
<math>0.005(s\mathcal{L}{i_2}-i_2(0))+\mathcal{L}\left\{i_2\right\}-\mathcal{L}\left\{i_1\right\}=0</math> |
|||
<math>\Rightarrow-500I_1(s)+[s+500]I_2(s)=0</math> |
|||
Solving for <math>I_2(s)</math> |
|||
<math>I_2(s)= \frac{6250}{s(s^2+500s+2500)}</math> |
|||
We find the partial decomposition |
|||
Let <math>I_2(s)= \frac{6250}{s(s^2+500s+2500)}=\frac{A}{s}+\frac{Bs+C}{s^2+500s+2500}</math> |
|||
<math>\Rightarrow6250=A(s^2+500s+2500)+(Bs+C)s</math> |
|||
<math>\Rightarrow62500=As^2+500As+2500A+Bs^2+Cs</math> |
|||
Comparing the coefficients we get |
|||
<math>A=\frac{5}{2},B=-5,C=-1250</math> |
|||
Thus |
|||
<math>I_2(s)=\frac{5}{2s}-\frac{5s+1250}{s^2+500s+2500}</math> |
|||
Now we do the same for <math>I_1</math> where we solve the function in terms of <math>I_1</math> and decomposing the partial fraction resulting in |
|||
<math>I_1(s)= \frac{25s+12500}{s(s^2+500s+2500)}=\frac{5}{s}-\frac{5s+2475}{s^2+500s+2500}</math> |
|||
In order to make it nicer on us we need to complete the square as follows |
|||
<math> s^2+500s+2500=0</math> |
|||
<math>\Rightarrow s^2+500s=-2500</math> |
|||
<math>\Rightarrow s^2+500s+\left(\frac{500}{2}\right)^2=-2500+\left(\frac{500}{2}\right)^2</math> |
|||
<math>\Rightarrow s^2+500s+62500=6000</math> |
|||
<math>\Rightarrow (s+250)^2-(100\sqrt{6})^2=0</math> |
|||
Thus |
|||
<math>I_2(s)=\frac{5}{2s}-5\frac{s+250}{(s+250)^2-(100\sqrt{6})^2}-\frac{5\sqrt{6}}{12}\frac{100\sqrt{6}}{(s+250)^2-(100\sqrt{6})^2}</math> |
|||
Taking the Inverse Laplace transform gives |
|||
<math>\mathcal{L}^{-1}\left\{I_2(s)\right\}= i_2(t) =\frac{5}{2}-5e^{-250t}cosh100\sqrt{6}t-\frac{5\sqrt{6}}{12}5e^{-250t}sinh100\sqrt{6}t</math> |
|||
==Initial Value Theorem== |
|||
<math>\lim_{s \to \infty}sI(s)=f(0^+)</math> |
|||
<math>\lim_{s \to \infty} s\frac{25s+12500}{s(s^2+500s+2500)}=i(0)</math> |
|||
<math> \Rightarrow i(0)=0</math> |
|||
<math>\lim_{s \to \infty}s\frac{6250}{s(s^2+500s+2500)}=i(0)</math> |
|||
<math> \Rightarrow i(0)=0</math> |
|||
==Final Value Theorem== |
|||
<math>\lim_{s \to 0}sI(s)=f(\infty)</math> |
|||
<math>\lim_{s \to \infty} s\frac{25s+12500}{s(s^2+500s+2500)}=i(\infty)</math> |
|||
<math>\Rightarrow i(\infty)=0</math> |
|||
<math>\lim_{s \to 0}s\frac{6250}{s(s^2+500s+2500)}=i(\infty)</math> |
|||
<math>\Rightarrow i(\infty)=0</math> |
|||
==Bode Plots== |
|||
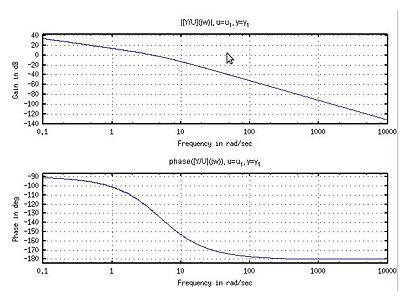
The following are bode plots for the transfer functions |
|||
[[Image:I1_.jpg|400px|thumb|left|<math>H(s)_1=\frac{25s+12500}{s(s^2+500s+2500)}</math>]] |
|||
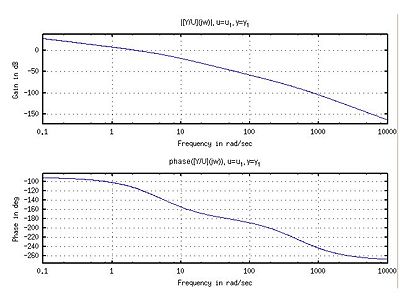
[[Image:I2_.jpg|400px|thumb|left|<math>H(s)_2=\frac{6250}{s(s^2+500s+2500)}</math>]] |
|||
Latest revision as of 16:35, 13 December 2009
Problem Statement
Using the formulas
Solve the system when V0 = 50 V, L = 4 h, R = 20 Ω, C = 10-4 f, and the currents are initially zero.
Solution
Solve the system when V0 = 50 V, L = 4 h, R = 20 Ω, C = 10-4 f, and the currents are initially zero.
Applying the Laplace transform to each equation gives
Solving for
We find the partial decomposition
Let
Comparing the coefficients we get
Thus
Now we do the same for where we solve the function in terms of and decomposing the partial fraction resulting in
In order to make it nicer on us we need to complete the square as follows
Thus
Taking the Inverse Laplace transform gives
Initial Value Theorem
Final Value Theorem
Bode Plots
The following are bode plots for the transfer functions







![{\displaystyle \Rightarrow -500I_{1}(s)+[s+500]I_{2}(s)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3baeaaedf034e407e6f24ab7df83d93f40383bf4)