Laplace transforms: Under-damped Mass-Spring System on an Incline

Brandon.plubell 05:44, 26 October 2009 (UTC)

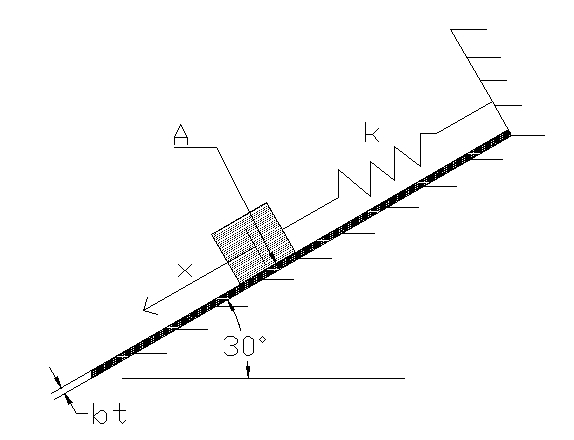
Under-Damped Mass-Spring System on an Incline

Part 1 - Use Laplace Transformations

Problem Statement

Find the equation of motion for the mass in the system subjected to the forces shown in the Free Body Diagram (FBD). The inclined surface is coated in SAE 30 oil.

Initial Conditions and Values

• A is the area of the box in contact with the surface
• g is the gravitational acceleration field constant
• b_t is the thickness of the fluid covering the inclined surface
• μ is the viscosity constant of the fluid;
• m is the mass of the box
• k is the spring constant

$A={\frac {1}{4}}m^{2}$

$g=9.81{\frac {m}{s^{2}}}$

$b_{t}=1mm{\frac {}{}}$

$\mu =0.06{\frac {N\cdot s}{m^{2}}}$

$m=45kg{\frac {}{}}$

$k=200{\frac {N}{m}}$

Let the initial conditions be:

$x(0)=-0.5m{\frac {}{}}$

${\dot {x}}(0)=0{\frac {m}{s}}$

Force Equations

The sum of the moments in the x direction yields the equatiom

$+\swarrow \sum F_{x}=m{\ddot {x}}$

$\Rightarrow \ m{\ddot {x}}=F_{s}+F_{f}+mg\sin \theta$

Where

$F_{s}=-k\,x$

$F_{f}=-{\frac {\mu \,A}{b_{t}}}\,{\dot {x}}$

To make the algebra easier, let

$\lambda ={\frac {\mu \,A}{b_{t}}}$

Then, from the sum of forces equation:

$m\,{\ddot {x}}+\lambda \,{\dot {x}}+k\,x=mg\sin \theta$

$\Rightarrow \ {\ddot {x}}+{\frac {\lambda }{m}}\,{\dot {x}}+{\frac {k}{m}}\,x=g\sin \theta$

Laplace Transform

${\mathcal {L}}\left\{{\ddot {x}}+{\frac {\lambda }{m}}\,{\dot {x}}+{\frac {k}{m}}\,x\right\}={\mathcal {L}}\left\{g\sin \theta \right\}$

$\Rightarrow \ s^{2}\,X(s)-s\,x(0)-x'(0)+{\frac {\lambda }{m}}\,s\,X(s)-{\frac {\lambda }{m}}\,x(0)+{\frac {k}{m}}\,X(s)=g\sin \theta \,\left({\frac {1}{s}}\right)$

$\Rightarrow \ X(s)\left(s^{2}+{\frac {\lambda }{m}}\,s+{\frac {k}{m}}\right)=g\sin \theta \,\left({\frac {1}{s}}\right)+s\,x(0)+x'(0)+{\frac {\lambda }{m}}\,x(0)$

If we let $x(0){\text{ and }}x'(0)$ be 0 and rearrange the equation,

${\frac {X(s)}{X_{in}(s)}}={\frac {X(s)}{g\sin \theta \left({\frac {1}{s}}\right)}}=H(s)$

$\Rightarrow H(s)={\frac {1}{s^{2}+{\frac {\lambda }{m}}\,s+{\frac {k}{m}}}}$

This is the transfer function that will be used in the Bode plot and provide valuable information about the system.

$X(s)=g\sin \theta \left({\frac {1}{s}}\right)\left({\frac {1}{s^{2}+{\frac {\lambda }{m}}\,s+{\frac {k}{m}}}}\right)+x(0)\,\left({\frac {s}{s^{2}+{\frac {\lambda }{m}}\,s+{\frac {k}{m}}}}\right)+x'(0)\,\left({\frac {1}{s^{2}+{\frac {\lambda }{m}}\,s+{\frac {k}{m}}}}\right)+{\frac {\lambda }{m}}\,x(0)\,\left({\frac {1}{s^{2}+{\frac {\lambda }{m}}\,s+{\frac {k}{m}}}}\right)$

Inverse Laplace Transform

Since the Laplace Transform is a linear transform, we need only find three inverse transforms. All of the these have complex roots, since ${\left({\frac {\lambda }{m}}\right)}^{2}<4\,{\frac {\lambda }{m}}$. Because I am not yet comfortable finding the inverse with complex roots by hand, I used a laplace transform program for the TI-89.

${\mathcal {L}}^{-1}\left\{{\frac {1}{s\left(s^{2}+{\frac {\lambda }{m}}\,s+{\frac {k}{m}}\right)}}\right\}=e^{{\frac {-1}{6}}\,t}\,\left[{\frac {-9}{40}}\cos {\left({\frac {{\sqrt {159}}\,t}{6}}\right)}-{\frac {3\,{\sqrt {159}}}{2120}}\,\sin {\left({\frac {{\sqrt {159}}\,t}{6}}\right)}\right]+{\frac {9}{40}}$

${\mathcal {L}}^{-1}\left\{{\frac {s}{s^{2}+{\frac {\lambda }{m}}\,s+{\frac {k}{m}}}}\right\}=e^{{\frac {-1}{6}}\,t}\,\left[\cos {\left({\frac {{\sqrt {159}}\,t}{6}}\right)}-{\frac {\sqrt {159}}{159}}\,\sin {\left({\frac {{\sqrt {159}}\,t}{6}}\right)}\right]$

${\mathcal {L}}^{-1}\left\{{\frac {1}{s^{2}+{\frac {\lambda }{m}}\,s+{\frac {k}{m}}}}\right\}=e^{{\frac {-1}{6}}\,t}\,\left[{\frac {2\,{\sqrt {159}}}{53}}\,\sin {\left({\frac {{\sqrt {159}}\,t}{6}}\right)}\right]$