The development of the DFT: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
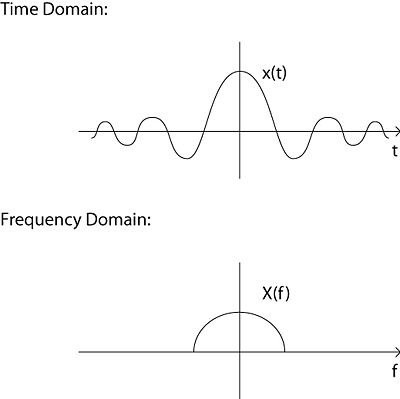
If we have a signal, such as following: |
If we have a signal, such as following: |
||
[[Image:DFT1.jpg]] |
[[Image:DFT1.jpg|400px]] |
||
How do we put it into computer? |
How do we put it into computer? |
||
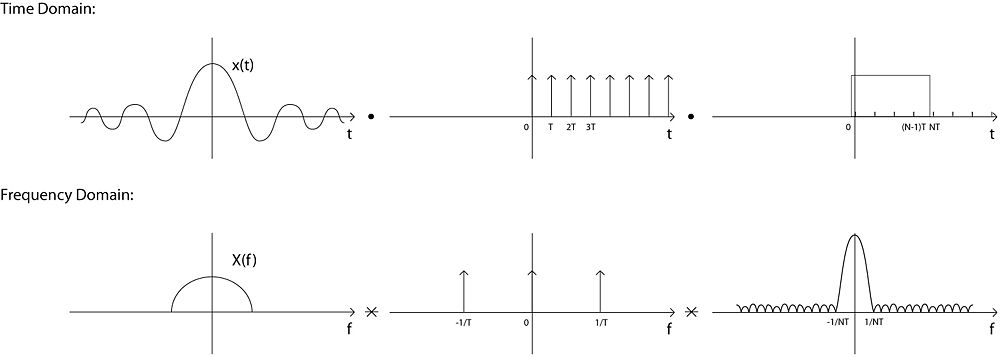
We can use A/D converter and a low pass filter to sample the signal with wanted instead of from t = -\infty to \infty: |
We can use A/D converter and a low pass filter to sample the signal with wanted instead of from t = -\infty to \infty: |
||
[[Image:DFT2.jpg]] |
[[Image:DFT2.jpg|1000px]] |
||
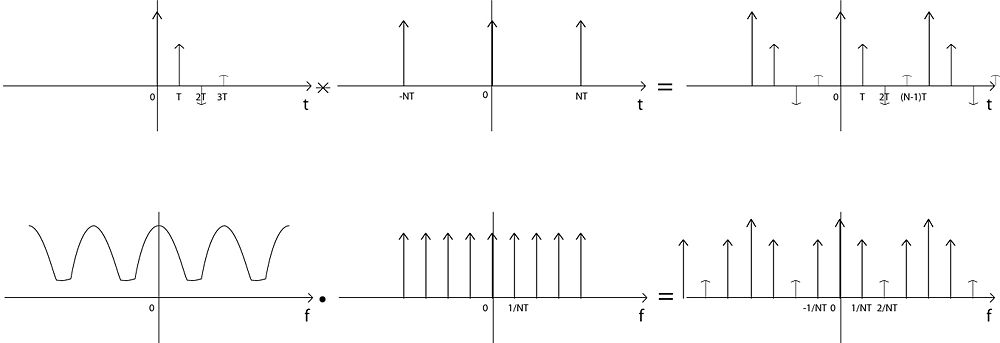
But then we have to make it periodic, so we convolve it with impulse function with NT apart to have impulse function in both time and frequency domain: |
But then we have to make it periodic, so we convolve it with impulse function with NT apart to have impulse function in both time and frequency domain: |
||
[[Image:DFT3.jpg]] |
[[Image:DFT3.jpg|1000px]] |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
Then the areas of the impulse functions is: |
|||
<math>\sum_{n=0}^{N-1}x(n)\, e^{-j2\pi\frac{nm}{N}}</math> |
|||
| ⚫ | |||
==Property of the DFT== |
|||
*DFT is periodic. |
|||
Proof: |
|||
<math>X(m+N)=\sum_{n=0}^{N-1}x(n)\, e^{-j2\pi\frac{n(m+N)}{N}}=\sum_{n=0}^{N-1}x(n)\, e^{-j2\pi\frac{nm}{N}}e^{-j2\pi\frac{nN}{N}}=\sum_{n=0}^{N-1}x(n)\, e^{-j2\pi\frac{nm}{N}}=X(m)</math> |
|||
==Inverse DFT== |
|||
Let's try to get back x(l) if we have X(m) |
|||
<math>X(m)=\sum_{n=0}^{N-1}x(n)\, e^{-j2\pi\frac{nm}{N}}</math> |
|||
Let's try do some trick to this DFT, let's sum it up and with exponents tag along. |
|||
<math>\sum_{m=0}^{N-1}X(m)\, e^{j2\pi\frac{lm}{N}} = \sum_{m=0}^{N-1}\sum_{n=0}^{N-1}x(n)\, e^{-j2\pi\frac{nm}{N}}e^{j2\pi\frac{lm}{N}}=\sum_{n=0}^{N-1}x(n)\sum_{m=0}^{N-1}e^{j2\pi\frac{(l-n)m}{N}}</math> |
|||
Note: <math>\sum_{m=0}^{N-1}e^{j2\pi\frac{(l-n)m}{N}}</math> will be N if <math>l=n</math>. |
|||
Let <math>e^{j2\pi\frac{(l-n)m}{N}}=r^m</math> then <math>r=e^{j2\pi\frac{(l-n)}{N}}</math> |
|||
So we know the sum of <math> r^m=S=1+r+r^2+r^3+...+r^{N-1}</math> |
|||
Therefore, we can divide r at both side of equation and get <math>\frac{S-1}{r}=S-r^{N-1}, S(\frac{1}{r}-1)=\frac{1}{r}-r^{N-1}, S=\frac{1-r^N}{1-r}</math> |
|||
Think about this, if <math>l\ne\, n, r=e^{j2\pi\frac{(l-n)}{N}}, S =\frac{1-e^{j2\pi(l-n)}}{1-e^{j2\pi\frac{(l-n)}{N}}}=0</math>, since <math>e^{j2\pi(l-n)}=1</math> for any integer of l and n. |
|||
So <math>\sum_{m=0}^{N-1}X(m)\, e^{j2\pi\frac{lm}{N}}=\sum_{n=0}^{N-1}x(n)N\delta_{n,l}=Nx(l)</math> |
|||
<math>x(l) = \frac{1}{N}\sum_{m=0}^{N-1}X(m)\, e^{j2\pi\frac{lm}{N}}\equiv\, IDFT(X(n)) </math> |
|||
Key points to note: |
|||
* By doing the DFT, we make the signal periodic in both time domain and frequency domain. |
|||
<math> X(m+N)=X(m),\,\, x(n+N)=x(n) </math> |
|||
* <math> X(m) \,\,for\,\,\, m>\frac{N}{2}</math> corresponds to <math> X(m-N)</math> |
|||
==Approximation of Fourier integral== |
|||
We can kind of see the DFT as an approximation to the Fourier integral. |
|||
<math>X(m)=\sum_{n=0}^{N-1}x(n)\, e^{-j2\pi\frac{nm}{N}}=\frac{1}{T}\sum_{n=-\frac{N}{2}}^{N-1-\frac{N}{2}}x(n)\, e^{-j2\pi\, nT\frac{m}{NT}}T\cong\frac{1}{T}\int_{-\frac{NT}{2}}^{\frac{NT}{2}}\,x(t)e^{-j2\pi\,tf}\,dt</math> |
|||
Revision as of 02:09, 20 November 2008
If we have a signal, such as following:
How do we put it into computer? We can use A/D converter and a low pass filter to sample the signal with wanted instead of from t = -\infty to \infty:
But then we have to make it periodic, so we convolve it with impulse function with NT apart to have impulse function in both time and frequency domain:
From the equations of final signal in both time and frequency domain, we can see that in the computer we have x(n) and in the frequency domain:
Then the areas of the impulse functions is:
Which is the definition of the .
Property of the DFT
- DFT is periodic.
Proof:
Inverse DFT
Let's try to get back x(l) if we have X(m)
Let's try do some trick to this DFT, let's sum it up and with exponents tag along.
Note: will be N if .
Let then
So we know the sum of
Therefore, we can divide r at both side of equation and get
Think about this, if , since for any integer of l and n.
So
Key points to note:
- By doing the DFT, we make the signal periodic in both time domain and frequency domain.
- corresponds to
Approximation of Fourier integral
We can kind of see the DFT as an approximation to the Fourier integral.