|
|
| Line 52: |
Line 52: |
|
So <math>\sum_{m=0}^{N-1}X(m)\, e^{j2\pi\frac{lm}{N}}=\sum_{n=0}^{N-1}x(n)N\delta_{n,l}=Nx(l)</math> |
|
So <math>\sum_{m=0}^{N-1}X(m)\, e^{j2\pi\frac{lm}{N}}=\sum_{n=0}^{N-1}x(n)N\delta_{n,l}=Nx(l)</math> |
|
|
|
|
|
<math>x(l) = \frac{1}{N}\sum_{m=0}^{N-1}X(m)\, e^{j2\pi\frac{lm}{N}}\equiv\, IDFT(X(n)) </math> |
|
<math>x(l) = \frac{1}{N}\sum_{m=0}^{N-1}X(m)\, e^{j2\pi\frac{lm}{N}}\equiv\, IDFT(X(m)) </math> |
|
|
|
|
|
Key points to note: |
|
Key points to note: |
If we have a signal, such as following:
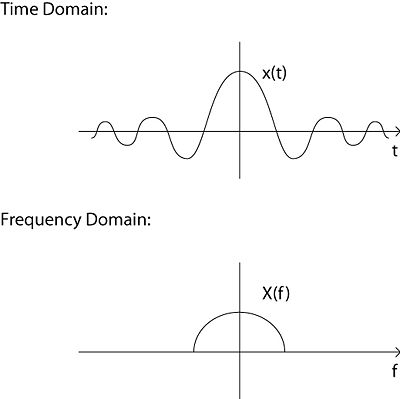
How do we put it into computer?
We can use A/D converter and a low pass filter to sample the signal that is wanted instead of from  :
:
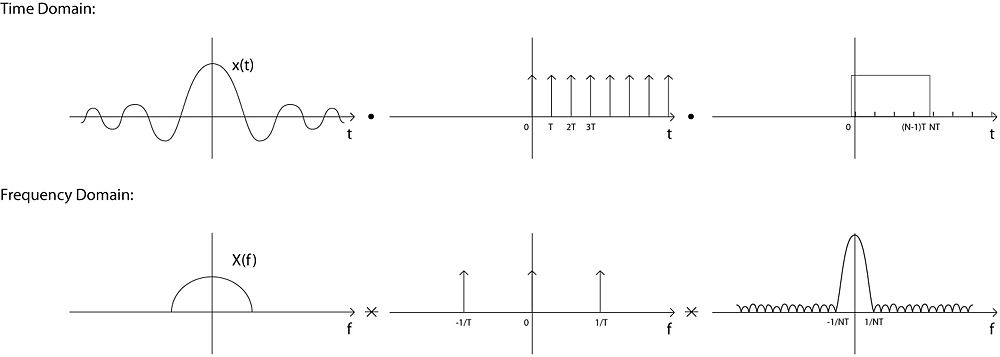
But then we have to make it periodic, so we convolve it with impulse function with NT apart to have impulse function in both time and frequency domain:
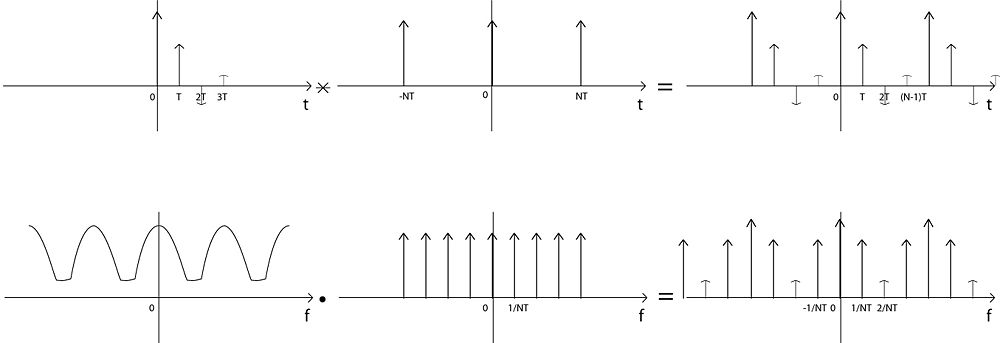
From the equations of final signal in both time and frequency domain, we can see that in the computer we have x(n) and in the frequency domain:

Then the areas of the impulse functions is:

Which is the definition of the  .
.
Property of the DFT
Proof:

Inverse DFT
Let's try to get back x(l) if we have X(m)

Let's try do some trick to this DFT, let's sum it up and with exponents tag along.

Note:  will be N if
will be N if  .
.
Let  then
then 
So we know the sum of 
Therefore, we can divide r at both side of equation and get 
Think about this, if  , since
, since  for any integer of l and n.
for any integer of l and n.
So 

Key points to note:
- By doing the DFT, we make the signal periodic in both time domain and frequency domain.

 corresponds to
corresponds to 
Approximation of Fourier integral
We can kind of see the DFT as an approximation to the Fourier integral.
























