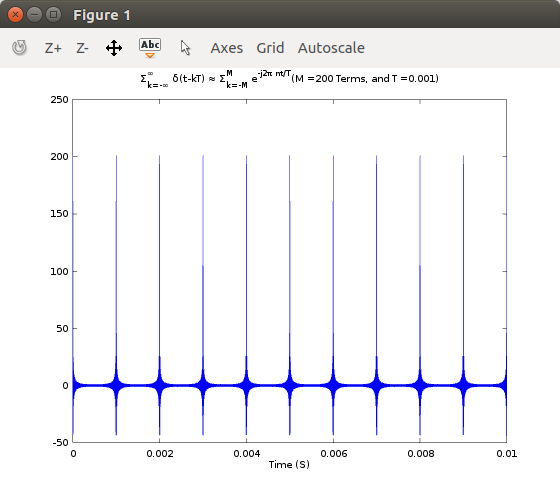
An octave/MATLAB script to show the Fourier series of a string of impulse functions
Jump to navigation
Jump to search
This checks this identity.
% This is a script to see if the Fourier series with unity coefficients is
% really a series of impulse functions.
M=100; % Number of terms
T=1e-3; % the period of the sampling function is 1 mS.
t=0:T/1000:10*T;
f=zeros(size(t));
for k=-M:M
v = 1;
f = f +v*exp(j*2*pi*k*t/T);
end
plot(t,f)
title(strcat('\Sigma_{k=-\infty}^\infty \delta(t-kT) \approx \Sigma_{k=-M}^M e^{-j2\pi nt/T}'
,'(M = ',num2str(2*M),' Terms, and T =',num2str(T),')'))
%title(strcat('Fourier Series of a Sum ofImpulse Functions with ',num2str(2*M),' Terms'))
xlabel('Time (S)')