Basic Op Amp circuits
Jump to navigation
Jump to search
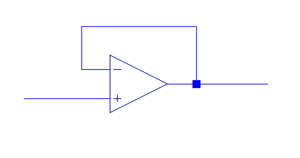
Buffer Amplifier
- Used to transfer voltage but not current to the following circuit. This amplifier can be used to negate the loading effects. No current flows through the amplifier, thus there is no voltage drop through the input resistor (going to the buffer amplifier).
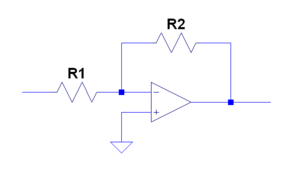
Inverting Amplifier
- Uses negative feedback to invert and amplify voltage. Using nodal analysis at the negative terminal, the gain is found to be
- To get rid of unwanted DC components, a capacitor can be added inbetween and . In this case
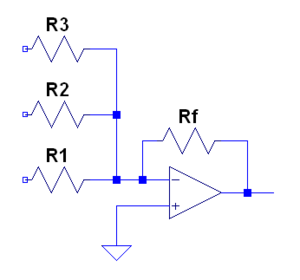
Summing Amplifier
- If all resistances are equal, then the output voltage is the (negative) sum of the input voltages
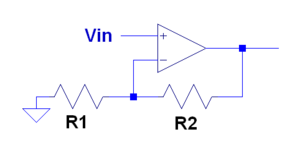
Noninverting Amplifier
- goes between the positive terminal and
- To get rid of unwanted DC components, a capacitor can be added inbetween the positive terminal and . The bias resistor has the same value, and is placed inbetween the positive input terminal and ground.
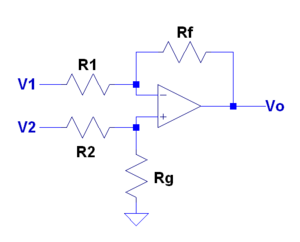
Differential Amplifier
- If you let and then the equation simplifies to
Possible circuits to add in the future
- Voltage-to-current converter
- Current-to-voltage converter
- Current amplifier
- Integrator
- Differentiator
Reviewers
- Victor Shepherd
- Michael Vier