Chapter 1

Amplifier Models

These are purely models, and cannot be replicated in a real world environment. They are meant to explain.
Trans stands for transfer (from voltage to current or visa versa).
The inputs and outputs can be either current or voltage. This leads to 4 amplifier models.
You can use any of these models, though some may be easier to work with (if you are given the Thevenin or Norton equivalent).

Amplifier models
Amplifier type Gain parameter Gain equation	Voltage input	Current input
Voltage output	Voltage Open-circuit voltage gain $A_{voc}={\frac {v_{ooc}}{v_{i}}}$	Transresistance Open-circuit transresistance gain $R_{moc}={\frac {v_{ooc}}{i_{i}}}$
Current output	Transconductance Short-circuit transconductance gain $G_{msc}={\frac {i_{osc}}{v_{i}}}$	Current Short-circuit current gain $A_{isc}={\frac {i_{osc}}{i_{i}}}$

Characteristics of ideal amplifiers
Amplifier Type	Input Impedance	Output Impedance	Gain Parameter
Voltage	$\infty$	0	$A_{voc}\,$
Current	0	$\infty$	$A_{isc}\,$
Transconductance	$\infty$	$\infty$	$G_{msc}\,$
Transresistance	0	0	$R_{moc}\,$

Differential Amplifier inputs

Differential amplifiers take two (or more) input sources and produce an output voltage proportional to the difference between the input voltages.
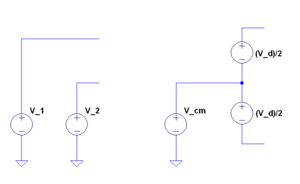
Instead of expressing the input voltages in terms of $v_{1}\,$ $v_{1}\,$ and $v_{i}\,$ $v_{i}\,$ , we can express them in terms of the differential and common-mode input.
- Differential input signal is the difference between the input voltages. $v_{d}=v_{1}-v_{2}\,$
- Common-mode input signal is the average of the input voltages. $v_{cm}={\frac {1}{2}}(v_{1}+v_{2})$
- $v_{1}=v_{cm}+{\frac {v_{d}}{2}}$ , if $v_{1}\,$ is voltage at the positive terminal.
- $v_{2}=v_{cm}-{\frac {v_{d}}{2}}$ , if $v_{2}\,$ is voltage at the negative terminal.
$v_{o}=A_{d}v_{d}+A_{cm}v_{cm}\,$ , where $A_{d}\,$ is the differential gain and $A_{cm}\,$ is the common mode gain.
The common-mode rejection ratio (CMRR) is the ratio of the magnitude of the differential gain to the magnitude of the common-mode gain.
- In decibels, $CMRR=20\log {\frac {|A_{d}|}{|A_{cm}|}}$

Input Resistance: $R_{i}$ of an amplifier is the equivalent resistance seen when looking into the input terminals.
Output Resistance: $R_{o}$ is the Thevenin resistance seen when looking back into the output terminals of an amplifier.
Open-circuit voltage gain: the ratio of output amplitude to input amplitude with the output terminals open circuited.
Short-circuit current gain: the current gain with the output terminals of the amplifier short circuited.

v(t)={\frac {q(t)}{C}}={\frac {1}{C}}\int _{t_{0}}^{t}i(\tau )\mathrm {d} \tau +v(t_{0})

i(t)={\frac {\mathrm {d} q(t)}{\mathrm {d} t}}=C{\frac {\mathrm {d} v(t)}{\mathrm {d} t}}

v(t)=L{\frac {di(t)}{dt}}

i(t)={\frac {1}{L}}\int _{t_{0}}^{t}v(\tau )d\tau +i({t_{0}})