Example Problems of Magnetic Circuits

Problem 1 Kevin Starkey

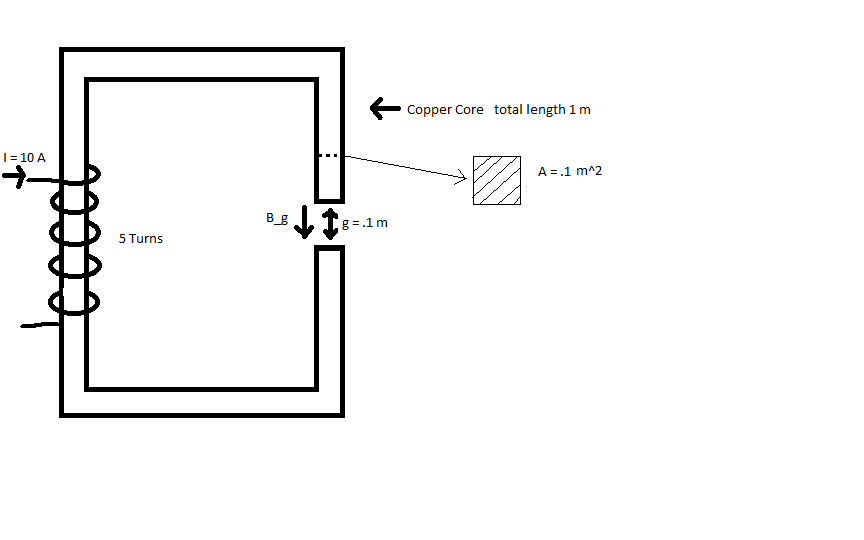
Given a copper core with:

Susceptibility $\chi _{m}=-9.7\times 10^{-6}$

Length of core L = 1 m

Gap length g = .01 m

Cross sectional area A = .1 m

Current I = 10A

N = 5 turns

Find: $B_{g}$

Solution: First we need to find the permeability of copper $\mu$ given by the equation
$\mu =\mu _{0}(1+\chi _{m})$

Which yeilds $\mu =4\times \pi \times 10^{-7}(1+-9.7\times 10^{-6})=1.2566\times 10^{-6}{\frac {N}{A^{2}}}$

Now using the length, cross sectional area, and permeability of the core we can solve for reluctance $R_{c}$ by:

$R_{c}={\frac {L}{\mu A}}={\frac {1}{1.2566\times 10^{-6}\times .1}}=7.96\times 10^{6}$

Similarly, to get the reluctance of the gap

$R_{g}={\frac {g}{\mu _{0}({\sqrt {A}}+g)^{2}}}={\frac {.01}{4\times \pi \times 10^{-7}({\sqrt {.1}}+.01)^{2}}}=74.8\times 10^{3}$

Now recall the equation for the magnetic field of a gap as seen in class $B_{g}={\frac {NI}{(R_{g}R_{c})(({\sqrt {A}}+g)^{2}}}$
Yields $B_{g}={\frac {5\times 10}{74.8\times 10^{3}\times 7.96\times 10^{6}\times ({\sqrt {.1}}+.01)^{2}}}=.789\times 10^{-9}$
This is the magnetic field in the center of the gap due to the applied current

Reviewers:

---

Nick Christman:

• I would change "Given: (...)[list] A copper core with..." to "Given a copper core with: [list]" to make it a little more consistent or even take all the information you have and make it into a complete sentence/paragraph.
• This looks strange to me, $\mu =4\times \pi \times 10^{-7}(1+-9.7\times 10^{-6})$ maybe make it $\mu =4\pi \times 10^{-7}(1-9.7\times 10^{-6})$ or $\mu =4\pi \times 10^{-7}(1+(-9.7\times 10^{-6}))$
• This sentence is kind of strange, "Now with this, the length and cross sectional area of the core we can solve for reluctance..." Maybe make it, "With the permeability, length, and cross sectional area of the copper core we can now solve for the reluctance..." Something like that might flow a little better."
• Below that, I think you need a comma after "Similarly."
• You might want to add some more words to the last two lines... Instead of saying "Now using..." say something like, "Recall that the equation for the magnetic field of the gap is..." or something to that effect.
• Lastly, you should think of some sort of conclusion... what exactly does this mean?