Exercise: Sawtooth Wave Fourier Transform

Problem Statement

Find the Fourier Tranform of the sawtooth wave given by the equation

$x(t)=t-\lfloor t\rfloor$

Solution

As shown in class, the general equation for the Fourier Transform for a periodic function with period $T$ is given by

$x(t)=\frac{a_0}{2}+\sum _{n=1}^{\mathrm{\infty }}[a_n\cos \frac{2\pi nt}{T}+b_n\sin \frac{2\pi nt}{T}]$

where

$$\begin{gathered} \{\begin{array}{l}{a}_n=\frac{2}{T}\underset{c}{\overset{c+T}{\int }}x(t)\cos \frac{2\pi nt}{T}dt\\ b_n=\frac{2}{T}\underset{c}{\overset{c+T}{\int }}x(t)\sin \frac{2\pi nt}{T}dt\end{array} \\ n=0,1,2,3\dots \end{gathered}$$

For the sawtooth function given, we note that $T=1$, and an obvious choice for $c$ is 0 since this allows us to reduce the equation to $x(t)=t$. It remains, then, only to find the expression for $a_n$ and $b_n$. We proceed first to find $b_n$.

$$\begin{gathered} b_n=\frac{2}{1}\underset{0}{\overset{1}{\int }}t\sin 2\pi nt \\ dt \end{gathered}$$

which is solved easiest with integration by parts, letting

$u=t\Rightarrow du=dt$

$$\begin{gathered} dv=\sin 2\pi nt \\ dt\Rightarrow v=-\frac{1}{2\pi n}\cos 2\pi nt \end{gathered}$$

so

$$\begin{gathered} b_n=2[t(-\frac{1}{2\pi n})\cos 2\pi nt{|}_0^1+\frac{1}{2\pi n}\underset{0}{\overset{1}{\int }}\cos 2\pi nt \\ dt] \end{gathered}$$

$=2[(-\frac{1}{2\pi n}\cos 2\pi n-0)+{\left(\frac{1}{2\pi n}\right)}^2\sin 2\pi nt{|}_0^1]$

$=2[-\frac{1}{2\pi n}(1)+0]$

$=-\frac{1}{\pi n}$

Now, for $a_n$ we must consider the case when $n=0$ separately.

$$\begin{gathered} a_0=\frac{2}{1}\underset{0}{\overset{1}{\int }}t \\ dt=t^2{|}_0^1=1 \end{gathered}$$

For $n=1,2,3\dots$, we have

$$\begin{gathered} a_n=\frac{2}{1}\underset{0}{\overset{1}{\int }}t\cos 2\pi nt \\ dt \end{gathered}$$

which again is best solved using integration by parts, this time with

$u=t\Rightarrow du=dt$

$$\begin{gathered} dv=\cos 2\pi nt \\ dt\Rightarrow v=\frac{1}{2\pi n}\sin 2\pi nt \end{gathered}$$

so

$$\begin{gathered} a_n=2[t\left(\frac{1}{2\pi n}\right)\sin 2\pi nt{|}_0^1-\underset{0}{\overset{1}{\int }}\frac{1}{2\pi n}\sin 2\pi nt \\ dt] \end{gathered}$$

$=2[(\frac{1}{2\pi n}\sin 2\pi n-0)-{[-{\left(\frac{1}{2\pi n}\right)}^2\cos 2\pi nt]}_0^1]$

$=2[0+{\left(\frac{1}{2\pi n}\right)}^2(\cos 2\pi n-\cos 0)]$

$=0$

Therefore, the Fourier Transform representation of the sawtooth wave given is:

$x(t)=\frac{1}{2}-\sum _{n=1}^{\mathrm{\infty }}\frac{1}{\pi n}\sin 2\pi nt$

Solution Graphs

The figures below graph the first few iterations of the above solution. The first graph shows the solution truncated after the first 100 terms of the infinite sum, as well as each of the contributing sine waves with offset. The second figure shows the function truncated after 1, 3, 5, 10, 50, and 100 terms. The last figure shows the Error between the Fourier Series truncated after the first 100 terms and the function itself. These figures were constructed using the following matlab code: SawToothFourier.

Error creating thumbnail: File missing

Error creating thumbnail: File missing

Error creating thumbnail: File missing

Solution as number of terms varies from 1 to 30.

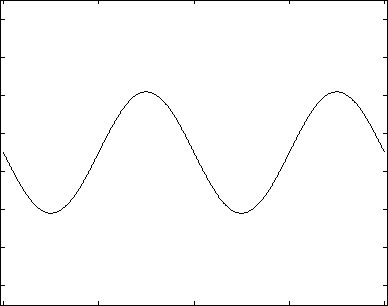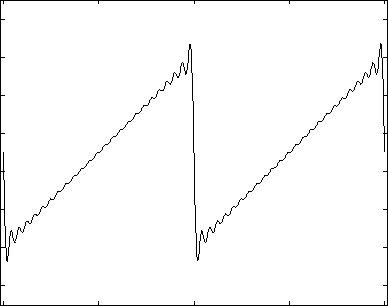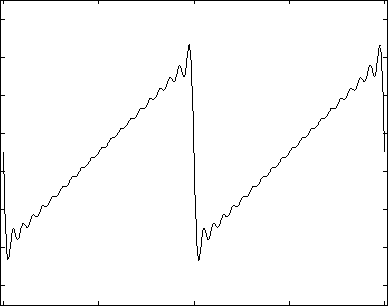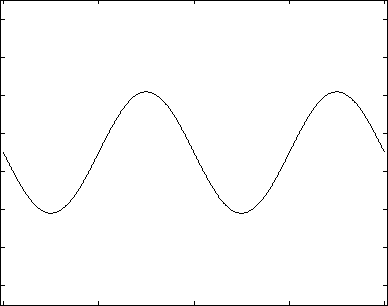
Author

John Hawkins

Read By

Christopher Garrison Lau I

Reviewed By

Colby Fullerton

• Michael Vier