Octave Simulation of a Tayloe Sampling Mixer
Jump to navigation
Jump to search
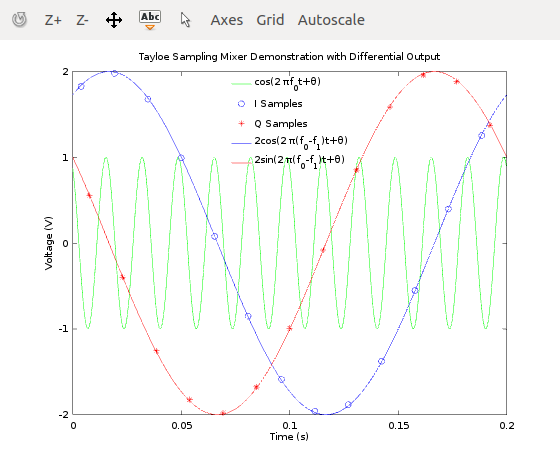
Here is a MATLAB/octave simulation of a Tayloe Sampling Mixer. It is useful to understand how the mixer works.
% This is to demonstrate the Tayloe Mixer.
clear all;
clf;
f0 = 60;
theta = pi/6; % Note: The phase doesn't match, except for 0 and pi. Direct
% conversion doesn't give the right sign on the imaginary part
f1 = 65;
T=0.0002;
N=1000;
t=0:T:(N-1)*T;
vin = cos(2*pi*f0*t+theta);
Ts = 1/4/f1;
t1 = 0:4*Ts:(N-1)*T;
vo1 = cos(2*pi*f0*t1+theta);
t2 = Ts:4*Ts:(N-1)*T+Ts;
vo2 = cos(2*pi*f0*t2+theta);
t3 = 2*Ts:4*Ts:(N-1)*T+2*Ts;
vo3 = cos(2*pi*f0*t3+theta);
t4 = 3*Ts:4*Ts:(N-1)*T+3*Ts;
vo4 = cos(2*pi*f0*t4+theta);
tI = 0:2*Ts:(N-1)*T;
voI = vo1-vo3; % Note: This is not quite right, because vo3 changes half a
% 2*Ts after vo1 does. The same thing happens with voQ. It
% looks pretty good for fl (and f0) high (>50 or so).
voQ = vo4-vo2;
plot(t,vin,'g-',t2,voI,'bo',t3,voQ,'r*',t,2*cos(2*pi*(f0-f1)*(t)+theta),'b-',t
,2*sin(2*pi*(f0-f1)*(t)+theta),'r-')
xlabel('Time (s)')
ylabel('Voltage (V)')
title('Tayloe Sampling Mixer Demonstration with Differential Output')
legend('cos(2 \pif_0t+\theta)','I Samples','Q Samples','2cos(2 \pi(f_0-f_1)t+\theta)',
'2sin(2 \pi(f_0-f_1)t+\theta)','Location','north')
legend('boxoff')