Superposition
Jump to navigation
Jump to search
Superposition
Superposition states that "any branch of a bilateral linear circuit having more than one independent source equals the algebraic sum of the responses caused by each independent source acting alone, while all other independent sources are replaced by their internal impedances."<ref> Wikipedia - Superposition </ref>
- Superposition allows us to analyze how each input source impacts the output.
- While building and debugging circuits, this is an invaluable tool. You can run through your circuit step-by-step to determine where your problems occurred.
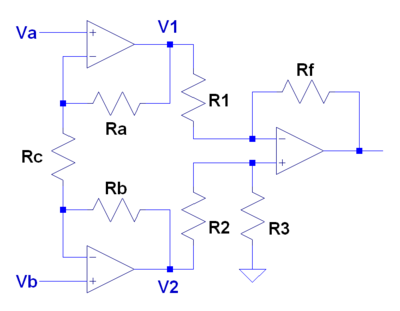
Dissecting an instrumentation quality differential amplifier via superposition
- Instead of trying to analyze the whole amplifier, we will break it down into two stages.
- Stage 1: A differential input/output amplifier
- Stage 2: A differential input amplifier
Stage 1
- Turn off first (arbitrarily chosen). Writing a nodal equation at the input terminals and solving for the unknown voltages.
- Turning off
- If a gain was desired for this stage, we could combine the previous 4 equations
Stage 2
- Turn off first (arbitrarily chosen). This makes the input terminals 0 volts. Once again writing nodal equations and solving for the unknown voltages.
- An inverting amplifier
- Turning off
- If the gain was desired for this stage, we could combine the previous equations
- While this equation looks daunting, making use of symmetry will often simplify the equation.
Questions
- What are the internal impedances of voltage and current sources?
- Should I rephrase Wikipedia into more layman terms?
References
<references/>