User:Goeari: Difference between revisions
Jump to navigation
Jump to search
| Line 47: | Line 47: | ||
The low pass filter then knocks the high frequencies out of the signal coming from the D/A converter, which smoothes out the edges of the reproduced sine wave <math>\hat x(t)</math> in time. This output waveform then drives the speaker, thereby recreating the original sound stored on the CD. | The low pass filter then knocks the high frequencies out of the signal coming from the D/A converter, which smoothes out the edges of the reproduced sine wave <math>\hat x(t)</math> in time. This output waveform then drives the speaker, thereby recreating the original sound stored on the CD. | ||
Contributing Authors: | |||
Todd Caswell | [[User:caswto|Todd Caswell]] | ||
[[User:goeari|Aric Goe]] | |||
Revision as of 19:16, 6 December 2004
Signals & Systems
Introduction
Becoming familiar with Wiki
Well, it all seems a little too convenitent to me.
Practicing TEX
- Simple Transformer Equation
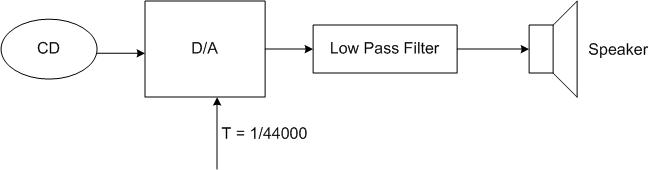
How a CD Player Works
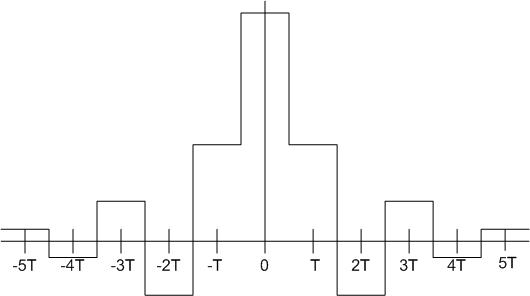
First, a digital signal is read from the CD and then convolved with a pulse function in the D/A converter. The result in the time domain looks like this:
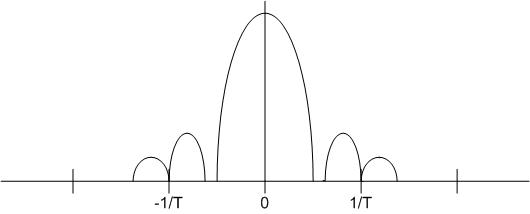
Let's look at this result in frequency space. Note that convolution in time means multiplication in frequency.
where
The low pass filter then knocks the high frequencies out of the signal coming from the D/A converter, which smoothes out the edges of the reproduced sine wave in time. This output waveform then drives the speaker, thereby recreating the original sound stored on the CD.
Contributing Authors: