DavidsCD: Difference between revisions
No edit summary |
|||
| (11 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
CD Players Explained! |
== CD Players Explained! == |
||
[[Image:davemic.gif]] |
|||
insert pic1 |
|||
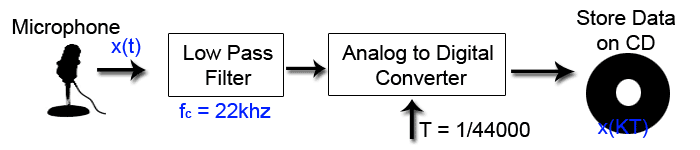
As seen above storing voice samles on a cd only involves a couple of steps. |
As seen above storing voice samles on a cd only involves a couple of steps. |
||
First the data must be passed through a low pass filter incase there are any unwanted high frequencies. In our case we would need a filter to pass anything under 22kHz. If we pass anything higher than this then there will be alaising. Next an analog to digital converter (ADC) samples the data at 44000kHz. It does this by basically picking the closest sampling value to the analog value. Next this data is stored on a CD. |
First the data must be passed through a low pass filter incase there are any unwanted high frequencies. In our case we would need a filter to pass anything under 22kHz. If we pass anything higher than this then there will be alaising. Next an analog to digital converter (ADC) samples the data at 44000kHz. It does this by basically picking the closest sampling value to the analog value. Next this data is stored on a CD. |
||
[[Image:davespk.gif]] |
|||
insert pic2 |
|||
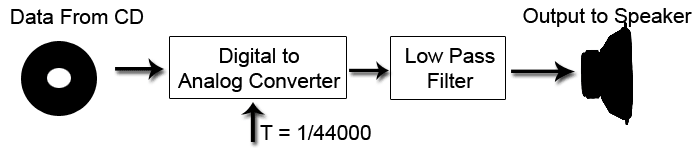
Data is taken from the CD player and is represented mathmatically as <math> \sum_{k= -\infty}^ \infty \ x(kT) \delta (t-KT) </math>. When the data goes through the Digital to Analog Converter (DAC) it is convolved with p(t) to get <math> \tilde x (t) = \sum_{k= -\infty}^ \infty \ x(kT) p (t-KT) </math> as shown below. |
Data is taken from the CD player and is represented mathmatically as <math> \sum_{k= -\infty}^ \infty \ x(kT) \delta (t-KT) </math>. When the data goes through the Digital to Analog Converter (DAC) it is convolved with p(t) to get <math> \tilde x (t) = \sum_{k= -\infty}^ \infty \ x(kT) p (t-KT) </math> as shown below. |
||
| Line 12: | Line 12: | ||
[[Image:barnsaDA.jpg|Digital to analog conversion]] |
[[Image:barnsaDA.jpg|Digital to analog conversion]] |
||
In the frequency domain you can see that this relates to multipliing <math> |
In the frequency domain you can see that this relates to multipliing <math> \frac{1}{T} \sum_{n=-\infty}^\infty X(f - \frac{n}{T}) \cdot </math> by P(f) and results in a quite distored X(f). It has to many high frequency components and would require a really good brick wall filter to get rid of them. From there the signal is sent to a Low Pass Filter where the stair stepped shaped function is smoothed so that it sounds better when the signal is next sent to the speaker. |
||
== Two Times Oversampling == |
|||
</center> |
|||
where |
|||
<center> |
|||
<math>P(f) = \int_{-\frac{T}{2}}^{\frac{T}{2}} e^{j2\pi ft} \, dt = T sinc(fT) |
|||
</math> |
|||
</center> |
|||
Oversampling is the process of interpolating data so that it looks like we have more data than we really do. Two times oversampling is accomplished by adding a digital interpolation filter right before the DAC. Now <math> \sum_{k= -\infty}^ \infty \ x(kT) \delta (t-KT) </math> is convolved with the desired impulse response. For two times oversampling it would be convolved with <math> h(lt/2) = \frac{T}{2} \int_{-\frac{-1}{T}}^{\frac{1}{T}} e^{(j 2 \pi l t f)/2} df </math> if we wanted to predistort the signal as well. This makes it so that the resulting wave in the frequency domain more closely matches the original signal. So we get more data points doing it this way, we get to filter the signal however we want, plus this allows for the use of a cheaper low pass filter since the frequency spacing is now 2/T. We just have to be sure and meet the Nyquist criteria now and sample the DAC at T/2 or 88kHz. |
|||
[[Image:barnsasample.jpg|Sampling a signal]] |
|||
<math> f(t) = \sum_{k= -\infty}^ \infty \alpha_k e^ \frac{j 2 \pi k t}{T} </math>. |
|||
Latest revision as of 23:43, 12 December 2005
CD Players Explained!
As seen above storing voice samles on a cd only involves a couple of steps. First the data must be passed through a low pass filter incase there are any unwanted high frequencies. In our case we would need a filter to pass anything under 22kHz. If we pass anything higher than this then there will be alaising. Next an analog to digital converter (ADC) samples the data at 44000kHz. It does this by basically picking the closest sampling value to the analog value. Next this data is stored on a CD.
Data is taken from the CD player and is represented mathmatically as . When the data goes through the Digital to Analog Converter (DAC) it is convolved with p(t) to get as shown below.
In the frequency domain you can see that this relates to multipliing by P(f) and results in a quite distored X(f). It has to many high frequency components and would require a really good brick wall filter to get rid of them. From there the signal is sent to a Low Pass Filter where the stair stepped shaped function is smoothed so that it sounds better when the signal is next sent to the speaker.
Two Times Oversampling
Oversampling is the process of interpolating data so that it looks like we have more data than we really do. Two times oversampling is accomplished by adding a digital interpolation filter right before the DAC. Now is convolved with the desired impulse response. For two times oversampling it would be convolved with if we wanted to predistort the signal as well. This makes it so that the resulting wave in the frequency domain more closely matches the original signal. So we get more data points doing it this way, we get to filter the signal however we want, plus this allows for the use of a cheaper low pass filter since the frequency spacing is now 2/T. We just have to be sure and meet the Nyquist criteria now and sample the DAC at T/2 or 88kHz.
