09/29 - Analogy to Vector Spaces: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
==Analogy to Vector Spaces== |
|||
Let the vector <math> \vec v </math> be defined as: |
Let the vector <math> \vec v </math> be defined as: |
||
*<math>\vec v = a_1 \cdot \hat v_1 + a_2 \cdot \hat v_2 + a_3 \cdot \hat v_3 = \sum_{j=1}^3 v_j \cdot \hat a_j </math> |
*<math>\vec v = a_1 \cdot \hat v_1 + a_2 \cdot \hat v_2 + a_3 \cdot \hat v_3 = \sum_{j=1}^3 v_j \cdot \hat a_j </math> |
||
| Line 4: | Line 5: | ||
**<math> \hat v_1, \hat v_2, \hat v_3 </math> are the basis vectors |
**<math> \hat v_1, \hat v_2, \hat v_3 </math> are the basis vectors |
||
**A vector basis is a set of n linearly independent vectors capable of generating? an n-dimensional subspace? of <math>\real^n</math> |
**A vector basis is a set of n linearly independent vectors capable of generating? an n-dimensional subspace? of <math>\real^n</math> |
||
==Dot Product & Inner Product== |
|||
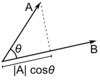
[[Image:300px-Dot_Product.svg.png|right|thumb|100px|Dot Product]] |
|||
The dot (scalar) product takes two vectors over the real numbers and returns a real-valued scalar quantity. Geometrically, it will show the projection of one vector onto another. |
The dot (scalar) product takes two vectors over the real numbers and returns a real-valued scalar quantity. Geometrically, it will show the projection of one vector onto another. |
||
Revision as of 12:53, 6 November 2008
Analogy to Vector Spaces
Let the vector be defined as:
-
- are the coefficients
- are the basis vectors
- A vector basis is a set of n linearly independent vectors capable of generating? an n-dimensional subspace? of
Dot Product & Inner Product
The dot (scalar) product takes two vectors over the real numbers and returns a real-valued scalar quantity. Geometrically, it will show the projection of one vector onto another.