The development of the DFT: Difference between revisions
Jump to navigation
Jump to search
(New page: <math>\sum_{m=1}^\infty\delta\left(t-nT\right)<\math> <math>\alpha\,\!</math>) |
No edit summary |
||
| Line 1: | Line 1: | ||
If we have a signal, such as following: |
|||
<math>\sum_{m=1}^\infty\delta\left(t-nT\right)<\math> |
|||
[[Image:DFT1.jpg]] |
|||
<math>\alpha\,\!</math> |
|||
How do we put it into computer? |
|||
We can use A/D converter and a low pass filter to sample the signal with wanted instead of from t = -\infty to \infty: |
|||
[[Image:DFT2.jpg]] |
|||
But then we have to make it periodic, so we convolve it with impulse function with NT apart to have impulse function in both time and frequency domain: |
|||
[[Image:DFT3.jpg]] |
|||
From the equations of final signal in both time and frequency domain, we can see that in the computer we have x(n) and in the frequency domain the areas of the impulse functions is: |
|||
<math>\sum_{m=-\infty}^\infty \frac{1} {NT}\sum_{n=0}^{N-1}X(nT)\, e^{-j2\pi\frac{m}{NT}nT} \delta\left(f-\frac{n}{NT}\right)</math> |
|||
Which is the definition of the DFT(x(n)). |
|||
Revision as of 00:00, 20 November 2008
If we have a signal, such as following:
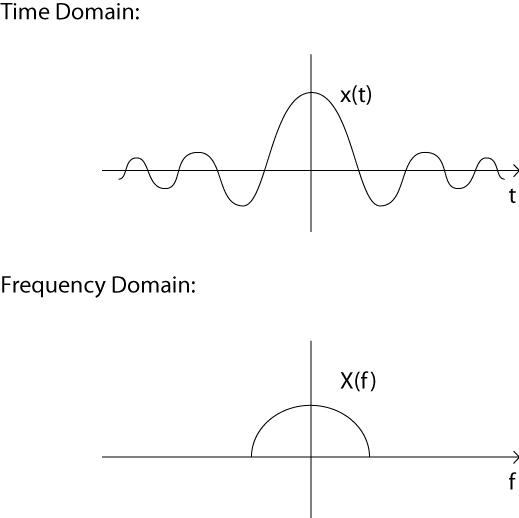How do we put it into computer?
We can use A/D converter and a low pass filter to sample the signal with wanted instead of from t = -\infty to \infty:
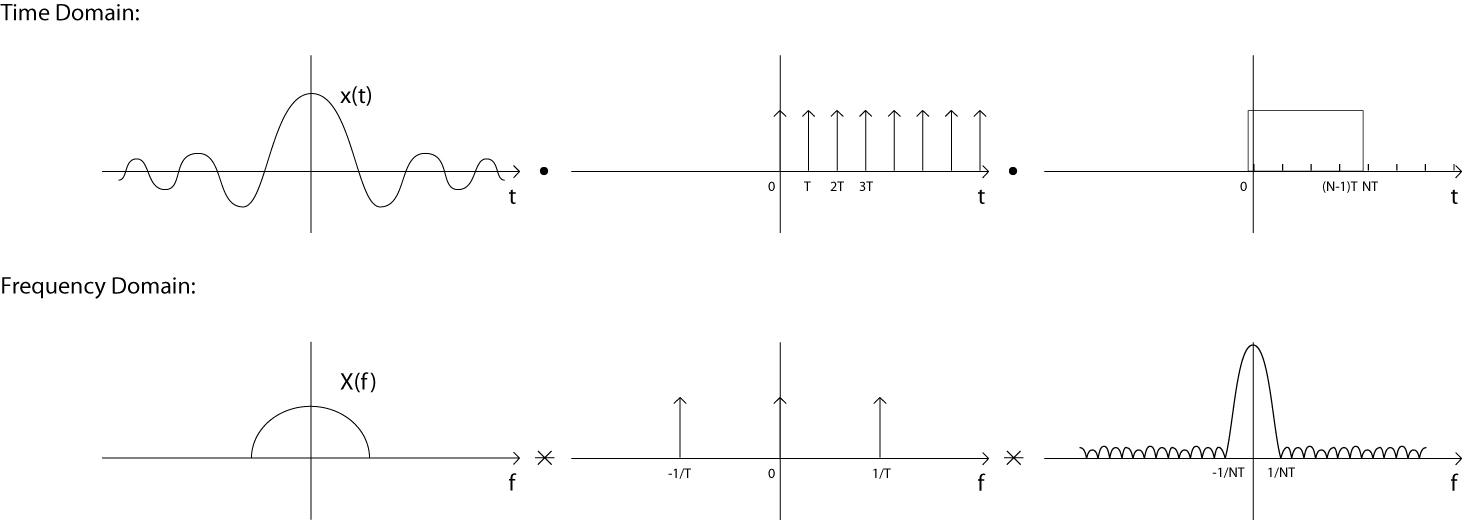But then we have to make it periodic, so we convolve it with impulse function with NT apart to have impulse function in both time and frequency domain:
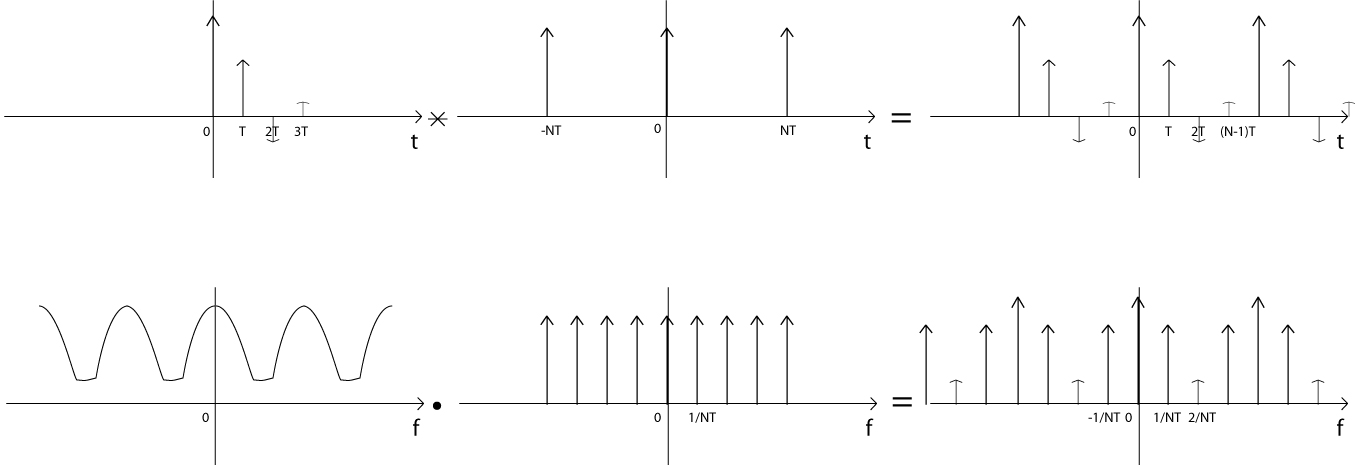From the equations of final signal in both time and frequency domain, we can see that in the computer we have x(n) and in the frequency domain the areas of the impulse functions is:
Which is the definition of the DFT(x(n)).
