DFT Developement (Brandon.Price)

The Fourier Transform is a powerful tool, but how can we use it (particularly with computers)?

Practical problems implementing the Fourier Transform

Let's take a look at the Fourier Transform and make some observations.

$X(f)={\mathcal {F}}(x(t))=\int _{-\infty }^{\infty }x(t)\ e^{-j2\pi tf}\,dt$

Here, we see an integration from a time of negative infinity to infinity for the function $x(t)$. This is a problem for several reasons:

1) We have no access to data for a given function before we start observing at t=0 (so we can't start at time = -$\infty$).

2) We don't want to wait until all time passes to compute the transform (so we can't start at time = $\infty$).

3) We can't use continuous integration since computers are restricted by finite memory.

We can get around each of these by noting that:

1) We don't care what happened to our signal before we started looking.

2) We don't care what happens to our signal after a certain (relatively short) length of time.

3) We can approximate an integral using a discrete summation (just like Riemann sums from the Calculus).

Our answer will not be the same as the true Fourier Transform, but as engineers, we are prepared to carefully sacrifice some precision for practicality. So, let's call this modification a "Discrete Fourier Transform (DFT)." How do we calculate one and how far does it stray from the Fourier Transform?

Extracting the DFT

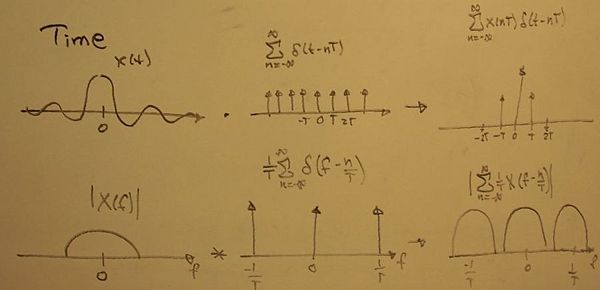
Let's start with an arbitrary continuous signal in time (and its corresponding frequency representation) and see how we might obtain our modified signal to be used in a computer. The pictures from class nicely describe the three steps (time domain on top and corresponding frequency domain on the bottom):

1) We start with an infinite continuous signal (in time) and multiply it by a sequence of delta functions, effectively sampling the continuous signal at discrete intervals. The resulting convolution in the frequency domain gives us a periodic frequency function.

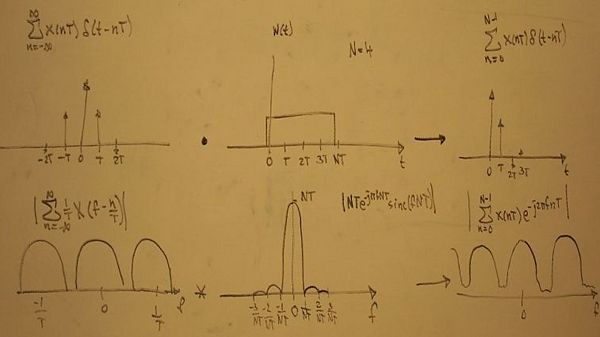
2) We multiply our infinite series of impulse functions by a windowing function (this eliminates the data before and after the length of time we care about). Now we have a discrete representation (N samples) of just the part of the signal we want. In the frequency domain, we once again convolve, resulting in a slightly distorted, periodic frequency signal. (Fewer samples or smaller sample interval results in more distortion in the frequency domain).

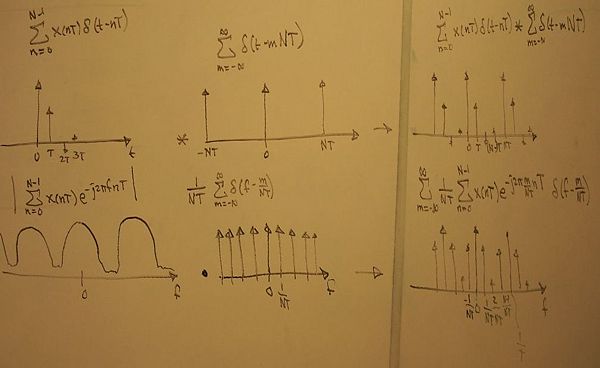
3) We want to work with discrete frequency data too, in the computer, so we multiply in the frequency domain by a sequence of impulse functions. The corresponding convolution in time makes our discrete sample periodic.

Now, we have a discrete representation of a small piece of the original continuous signal - both in time and frequency! Comparing the time domain and frequency domain, we can see the the DFT must be defined as:

$X(m)=DFT(x(nT))=\sum _{n=0}^{N-1}x(nT)\ e^{-j2\pi nm/N}$ for $m=0,\dots ,N-1$

Although it is slightly confusing, we usually represent x(nT) as simply x(n).

Properties of the DFT

Let us reflect on the DFT above...

*Periodicity*

We notice that X(m) is periodic with period N since:

$X(m+N)=\sum _{n=0}^{N-1}x(nT)\ e^{-j2\pi n(m+N)/N}=\sum _{n=0}^{N-1}x(nT)\ e^{-j2\pi nm/N}e^{-j2\pi n}=\sum _{n=0}^{N-1}x(nT)\ e^{-j2\pi nm/N}=X(m)$

*Fourier Integral Resemblance*

We notice that with the following approximations, we can see a resemblance between the DFT and the Fourier Integral:

$f\approx {\frac {m}{NT}}$

$t\approx nT$

$\int dt\approx \sum T$

So, slipping these into the DFT and shifting our index by N/2 (since the sequence is periodic) we find:

$DFT(x(nT))=\sum _{n=0}^{N-1}x(nT)\ e^{\frac {-j2\pi nm}{N}}={\frac {1}{T}}\sum _{n=-N/2}^{N/2-1}x(nT)\ e^{-j2\pi nT({\frac {m}{NT}})}T\approx {\frac {1}{T}}\int _{-NT/2}^{NT/2}x(t)\ e^{-j2\pi tf}\,dt$

The only real differences are limits on the integral and the 1/T scaling factor. So, the DFT may not be such a bad approximation after all!

*Inverse DFT (IDFT)*

Suppose we know X(n) for integer values of n. Can we extract x(m)? By definition,

$X(n)=\sum _{m=0}^{N-1}x(m)e^{\frac {-j2\pi nm}{N}}$ for $n\in \{0,1,2,\dots ,N-1\}$

Now, we start manipulating X(m), and hopefully arrive back at x(n):

$\sum _{n=0}^{N-1}X(n)e^{\frac {j2\pi ln}{N}}=\sum _{n=0}^{N-1}\sum _{m=0}^{N-1}x(m)e^{\frac {-j2\pi nm}{N}}e^{\frac {j2\pi ln}{N}}=\sum _{m=0}^{N-1}x(m)\sum _{n=0}^{N-1}e^{{\frac {j2\pi n}{N}}(l-m)}$

Now, using rather sneaky summation techniques from calculus (see webpage), we find

$\sum _{n=0}^{N-1}e^{{\frac {j2\pi n}{N}}(l-m)}=N\delta _{m,l}$

Applying this to our earlier equation, we have:

$\sum _{m=0}^{N-1}x(m)\sum _{n=0}^{N-1}e^{{\frac {j2\pi n}{N}}(l-m)}=\sum _{m=0}^{N-1}x(m)N\delta _{m,l}=Nx(l)$

Thus, since l is a dummy index just like n was, we find:

$IDFT(X(m))={\frac {1}{N}}\sum _{n=0}^{N-1}X(n)e^{\frac {j2\pi ln}{N}}=x(l)$

*Multiplication*

We saw earlier (for the Fourier Integral) that multiplying functions in the frequency domain corresponded to convolving the functions in the time domain (and vice versa). What happens in the discrete world with the DFT?

Let's take the IDFT of two frequency sequences:

$IDFT(X(n)H(n))=\sum _{n=0}^{N-1}{\frac {1}{N}}X(n)H(n)e^{\frac {-j2\pi kn}{N}}=\sum _{n=0}^{N-1}{\frac {1}{N}}\sum _{m=0}^{N-1}x(m)e^{\frac {-j2\pi nm}{N}}\sum _{l=0}^{N-1}h(l)e^{\frac {-j2\pi nl}{N}}e^{\frac {j2\pi kn}{N}}$

$={\frac {1}{N}}\sum _{m=0}^{N-1}x(m)\sum _{l=0}^{N-1}h(l)\sum _{n=0}^{N-1}e^{{\frac {j2\pi n}{N}}(k-l-m)}={\frac {1}{N}}\sum _{m=0}^{N-1}x(m)\sum _{l=0}^{N-1}h(l)N\delta _{l,k-m}=\sum _{m=0}^{N-1}x(m)h(k-m)$

This looks very similar to a convolution, and we call it a "Circular Convolution" since it only works when the sequences are periodic.