Laplace transforms:Series RLC circuit

Laplace Transform Example: Series RLC Circuit

Problem

Given a series RLC circuit with $R=10Ohms$, $L=0.1H$, and $C=10^{-5}F$, having power source $v(t)=10cos(20t)$, find an expression for $i(t)$ if $i(0)=0A$ and $v_{c}(0)=0V$.

Solution

We begin with the general formula for voltage drops around the circuit:

$v(t)=Ri+L{\dfrac {di}{dt}}+{\dfrac {1}{C}}\int {idt}$

Substituting numbers, we get

$10cos(20t)=10i+0.1{\dfrac {di}{dt}}+10^{5}\int {idt}$

$\Rightarrow cos(20t)=i+0.01{\dfrac {di}{dt}}+10000\int {idt}$

Now, we take the Laplace Transform and get

${\dfrac {s}{s^{2}+20^{2}}}=I+0.01[sI-i(0)]+10000{\dfrac {I}{s}}$

Using the fact that $i(0)=0A$, we get

${\dfrac {s}{s^{2}+400}}=I+0.01sI+10000{\dfrac {I}{s}}$

$\Rightarrow {\dfrac {s^{2}}{s^{2}+400}}=sI+0.01s^{2}I+10000I$

$\Rightarrow {\dfrac {s^{2}}{s^{2}+400}}=(0.01s^{2}+s+10000)I$

$\Rightarrow I(s)={\dfrac {s^{2}}{(s^{2}+400)(0.01s^{2}+s+10000)}}$

Using partial fraction decomposition, we find that

$I(s)={\dfrac {1.0004-4.003*10^{-8}s}{0.01s^{2}+s+10000}}+{\dfrac {4.003*10^{-6}s-0.04002}{s^{2}+400}}$

$\Rightarrow I(s)={\dfrac {100.04-4.003*10^{-6}s}{s^{2}+100s+1000000}}+{\dfrac {4.003*10^{-6}s-0.04002}{s^{2}+400}}$

$\Rightarrow I(s)={\dfrac {100.04-4.003*10^{-6}s}{(s+50)^{2}+997500}}+{\dfrac {4.003*10^{-6}s-0.04002}{s^{2}+400}}$

$\Rightarrow I(s)={\dfrac {100.038}{(s+50)^{2}+(50{\sqrt {399}})^{2}}}-{\dfrac {4.003*10^{-6}s+.002}{(s+50)^{2}+(50{\sqrt {399}})^{2}}}+{\dfrac {4.003*10^{-6}s}{s^{2}+20^{2}}}-{\dfrac {0.04002}{s^{2}+20^{2}}}$

$\Rightarrow I(s)={\dfrac {10.038}{50{\sqrt {399}}}}{\dfrac {50{\sqrt {399}}}{(s+50)^{2}+(50{\sqrt {399}})^{2}}}-4.003*10^{-6}{\dfrac {s+50}{(s+50)^{2}+(50{\sqrt {399}})^{2}}}+4.003*10^{-6}{\dfrac {s}{s^{2}+20^{2}}}-{\dfrac {0.04002}{20}}{\dfrac {20}{s^{2}+20^{2}}}$

Finally, we take the inverse Laplace transform to obtain

$i(t)=0.01e^{-50t}sin(998.8t)-(4.003*10^{-6})e^{-50t}cos(998.8t)+(4.003*10^{-6})cos(20t)-0.002sin(20t)\,$

which is our answer.

Initial/Final Value Theorems

We now want to use the Initial and Final Value Theorems on this problem.

The Initial Value Theorem states that

$\lim _{s\to \infty }sF(s)=f(0^{+})$

$\Rightarrow \lim _{s\to \infty }{\dfrac {s^{3}}{(s^{2}+400)(0.01s^{2}+s+10000)}}=i(0)$

$\Rightarrow i(0)=0$

In addition, when we actually evaluate $i(0)$ from our equation for $i(t)$, we find it to be 0 as well. So, things check out there.

The Final Value Theorem states that

$\lim _{s\to 0}sF(s)=f(\infty )$

$\Rightarrow \lim _{s\to 0}{\dfrac {s^{3}}{(s^{2}+400)(0.01s^{2}+s+10000)}}=i(\infty )$

$\Rightarrow i(\infty )=0$

This time, when we actually evaluate i(∞) from the equation for $i(t)$, we find it to be undefined. So here, the Final Value Theorem tells us something that is not necessarily true (in fact, because we have oscillating functions, we know that i(∞) will not be zero).

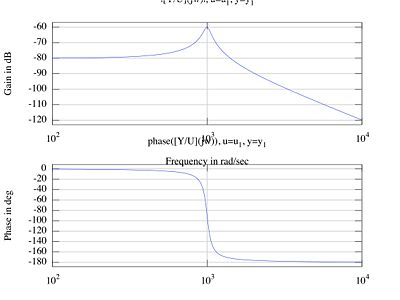
Bode Plot

To get a Bode plot, we use the transfer function:

$H(s)={\dfrac {s^{2}}{(s^{2}+400)(0.01s^{2}+s+10000)}}={\dfrac {s^{2}}{0.01s^{4}+s^{3}+10004s^{2}+400s+4000000}}$

We then use a program such as Octave or MATLAB to obtain the Bode plot, which looks like this:

Bode Plot

---

Written by Nathan Reeves ~ Checked by