Laplace transforms: Critically Damped Motion

Using the Laplace Transform to solve a spring mass system that is critically damped

Problem Statement

An 8 pound weight is attached to a spring with a spring constant k of 4 lb/ft. The spring is stretched 2 ft and rests at its equilibrium position. It is then released from rest with an initial upward velocity of 3 ft/s. The system contains a damping force of 2 times the initial velocity.

Solution

Things we know

$m={\frac {8}{32}}={\frac {1}{4}}slugs$

${\text{k=4}}\,$

${\text{Damping constant C=2}}\,$

${\text{x(0)=0}}\,$

${\dot {x}}(0)=-3$

${\text{Standard equation: }}\,$ $m{\frac {d^{2}x}{dt^{2}}}+C{\frac {dx}{dt}}+khx=0$

Solving the problem

${\text{Therefore the equation representing this system is.}}\,$

${\frac {1}{4}}{\frac {d^{2}x}{dt^{2}}}=-4x-2{\frac {dx}{dt}}$

${\text{Now we put the equation in standard form}}\,$

${\frac {d^{2}x}{dt^{2}}}+8{\frac {dx}{dt}}+16x=0$

${\text{Now that we have the equation written in standard form we need to send}}\,$ ${\text{it through the Laplace Transform.}}\,$

${\mathcal {L}}[{\frac {d^{2}x}{dt^{2}}}+8{\frac {dx}{dt}}+16x]$

${\text{And we get the equation (after some substitution and simplification)}}.\,$

$\mathbf {s} ^{2}{X}(s)+8\mathbf {s} {X}(s)+16\mathbf {X} (s)=-3$

$\mathbf {X} (s)(s^{2}+8s+16)=-3$

$\mathbf {X} (s)=-{\frac {3}{(s+4)^{2}}}$

${\text{Now that we have completed the Laplace Transform}}\,$ ${\text{and solved for X(s) we must so an inverse Laplace Transform. }}\,$

${\mathcal {L}}^{-1}[-{\frac {3}{(s+4)^{2}}}]$

${\text{and we get}}\,$

$\mathbf {x} (t)=-3te^{-4t}$

${\text{So there you have it the equation of a Critically Damped spring mass system.}}\,$

Apply the Initial and Final Value Theorems to find the initial and final values

Initial Value Theorem

$\lim _{s\rightarrow \infty }sF(s)=f(0)\,$

Final Value Theorem

$\lim _{s\rightarrow 0}sF(s)=f(\infty )\,$

Applying this to our problem

${\text{The Initial Value Theorem}}\,$

$\lim _{s\rightarrow \infty }\mathbf {sX} (s)=-{\frac {3}{(s+4)^{2}}}\,$

$\lim _{s\rightarrow \infty }\mathbf {s} {X}(s)=-{\frac {3}{(\infty +4)^{2}}}=0\,$

${\text{So as you can see the value for the initial position will be 0. }}\,$

${\text{Which makes sense because the system is initially in equilibrium. }}\,$

${\text{The Final Value Theorem}}\,$

$\lim _{s\rightarrow 0}\mathbf {s} {X}(s)=-{\frac {3}{(s+4)^{2}}}\,$

$\lim _{s\rightarrow 0}\mathbf {s} {X}(s)=-{\frac {3}{(0+4)^{2}}}=-{\frac {3}{16}}\,$

${\text{This shows the final value to be}}\,$ $-{\frac {3}{16}}ft$

${\text{Which appears to mean the system will be below equilibrium after a long time. }}\,$

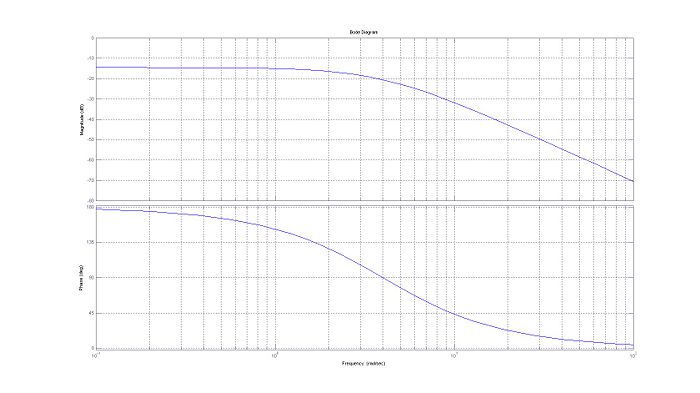
Bode Plot of the transfer function

Transfer Function

$\mathbf {X} (s)=-{\frac {3}{(s+4)^{2}}}$

Bode Plot

${\text{This plot is done using the control toolbox in MatLab. }}\,$

Fig (1)

     ==Break Points and Asymptotes==                                                                                                                                                      

${\text{A break point is defined by a place in the bode plot where a change occurs.}}\,$

${\text{To find your break points you must start with a transfer function. }}\,$

${\text{Transfer Function: }}\,$

$\mathbf {X} (s)=-{\frac {3}{(s+4)^{2}}}$

${\text{A break point is located at any value where s = what is being added to it. }}\,$ ${\text{So for this transfer function its at s=4 (that is also the asymptotes location). }}\,$

Convolution

${\text{The convolution equation is as follows: }}\,$

$x(t)=x_{in}(t)*h(t)=\int _{0}^{t}{x(t_{0})\,h(t-t_{0})\,dt_{0}}$

${\text{It does basically the same thing as the Laplace Transform. }}\,$ ${\text{To start we must inverse transform our transfer function }}\,$

$\mathbf {X} (s)=-{\frac {3}{(s+4)^{2}}}$

${\text{Which once more yields: }}\,$

$\mathbf {x} (t)=-3te^{-4t}$

${\text{Then we put this into the convolution integral: }}\,$

$x(t)=x_{in}(t)*h(t)=\int _{0}^{t}{-3(t-t_{0})e^{-4t-t_{0}}\,dt_{0}}$

${\text{Which once more yeilds: }}\,$

$\mathbf {x} (t)=(-cte^{-4t})$

${\text{Not exactly the same but remember initial conditions arnt used}}\,$ ---

Written By: Mark Bernet

Error Checked By: Greg Peterson