Homework Eight

How does a CD player work with no oversampling, but digital filtering (1x oversampling)?

Nick Christman

---

Recall that when the audio for a music CD is produced it has an infinite amount of data points which can be expressed as $x(t)$ in the time domain (Figure 1) and $X(f)$ in the frequency domain (Figure 2).

Figure 1: Audio data as a function of time, x(t)

Figure 2: Audio data as a function of frequency, X(f)

When one wants to store the data of $x(t)$ (i.e. reading the data onto a CD in this case) an infinite number of data points is not ideal -- in fact, it is impossible. Therefore, we must sample the data at the (typical) rate of $f_{s}={\frac {1}{T}}$. This will give us a periodic function which we will call $x(nT){\mbox{, where }}n\in \mathbb {Z} {\mbox{ and }}T$ is the sampling period. It is common to allow a sampling rate of twice the frequency at which a human can hear (i.e. 2 x 22 kHz) -- that means, $f_{s}=44$ kHz.

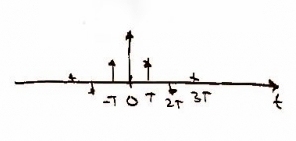
Recall from class that in order to sample the original function, $x(nT)$, we need to use a delta function. In other words, the continuous function of $x(nT)$ can be written as $\sum _{-\infty }^{\infty }x(nT)\delta (t-nT_{0})$ (Figure 3)

Figure 3: x(nT) written as impulses for sampling purposes