Homework Eight: Difference between revisions
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
---- |
---- |
||
Recall that when the audio for a music CD is produced it has an infinite amount of data points which can be expressed as <math>x(t)</math> in the time domain |
Recall that when the audio for a music CD is produced it has an infinite amount of data points which can be expressed as <math>\scriptstyle x(t)</math> in the time domain ['''Figure 1'''] and <math>\scriptstyle X(f)</math> in the frequency domain ['''Figure 2''']. |
||
[[Image:x_continuous3.jpg |thumb|center|upright=2|Figure 1: Audio data as a function of time, x(t)]] |
[[Image:x_continuous3.jpg |thumb|center|upright=2|Figure 1: Audio data as a function of time, x(t)]] |
||
[[Image:x_frequency1b.jpg |thumb|center|upright=2|Figure 2: Audio data as a function of frequency, X(f)]] |
[[Image:x_frequency1b.jpg |thumb|center|upright=2|Figure 2: Audio data as a function of frequency, X(f)]] |
||
When one wants to store the data of <math>x(t)</math> (i.e. reading the data onto a CD in this case) an infinite number of data points is not ideal -- in fact, it is impossible. Therefore, we must sample the data at the (typical) rate of <math>f_{s} = \frac{1}{T}</math>. This will give us a periodic function which we will call <math>x(nT) \mbox{, where } n \in \mathbb{Z} \mbox{ and } T</math> is the sampling period. It is common to allow a sampling rate of twice the frequency at which a human can hear (i.e. 2 x 22 kHz) -- that means, <math>f_{s} = 44</math> kHz.<br/> |
When one wants to store the data of <math>\scriptstyle x(t)</math> (i.e. reading the data onto a CD in this case) an infinite number of data points is not ideal -- in fact, it is impossible. Therefore, we must sample the data at the (typical) rate of <math>\scriptstyle f_{s} = \frac{1}{T}</math>. This will give us a periodic function which we will call <math>\scriptstyle x(nT) \mbox{, where } n \in \mathbb{Z} \mbox{ and } T</math> is the sampling period. It is common to allow a sampling rate of twice the frequency at which a human can hear (i.e. 2 x 22 kHz) -- that means, <math>\scriptstyle f_{s} = 44</math> kHz.<br/> |
||
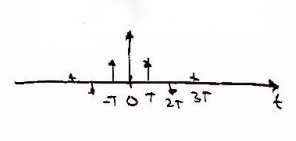
Recall from class that in order to sample the original function, <math>x(nT)</math>, we need to use a delta function. In other words, the continuous function of <math>x(nT)</math> can be written as <math>\sum_{-\infty}^{\infty}x(nT) \delta (t-nT_{0})</math> |
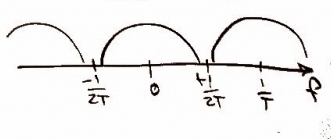
Recall from class that in order to sample the original function, <math>\scriptstyle x(nT)</math>, we need to use a delta function. In other words, the continuous function of <math>\scriptstyle x(nT)</math> can be written as <math> \sum_{n=-\infty}^{\infty}x(nT) \delta (t-nT_{0})</math> ['''Figure 3''']. As one may expect, in the frequency domain we should get the same plot as in '''Figure 2''', but it should repeat. In the frequency domain, this can be expressed as <math>\frac{1}{T}\sum_{n=-\infty}^{\infty}X(f-\frac{n}{T})</math> ['''Figure 4''']. |
||
[[Image:x_discrete_a.jpg |thumb|center|upright=2|Figure 3: x(nT) written as impulses for sampling purposes]] |
[[Image:x_discrete_a.jpg |thumb|center|upright=2|Figure 3: x(nT) written as impulses for sampling purposes]] |
||
[[Image:x_frequency2a.jpg |thumb|center|upright=2|Figure 4: x(nT) written as impulses for sampling purposes in the frequency domain]] |
|||
As one may suspect, in order to get a more accurate function you must take more data points -- in other words, a higher sampling rate (i.e. 2x, 8x, etc. oversampling) leads to a more accurate collection of data. For this case, we are asked to looked a digital sampling, or 1x oversampling. In order to accomplish this, we will convolve our function from above with a Finite Impulse Response filter (FIR filter). Let's call it g(t and define it as <math>\sum_{-M}^{M}g(\frac{mT}{p})\delta (t-\frac{mT}{p}) </math> where <math>\scriptstyle p</math> is the oversampling rate. In our case <math>\scriptstyle p = 1</math>. Because we are dealing with digital sampling, the convolution will result in the original function ['''Figure 5''']. |
|||
[[Image:x_discrete_a.jpg |thumb|center|upright=2|Figure 5: x(nT) after the convolution mentioned above]] |
|||
Revision as of 19:17, 8 November 2009
How does a CD player work with no oversampling, but digital filtering (1x oversampling)?
Recall that when the audio for a music CD is produced it has an infinite amount of data points which can be expressed as in the time domain [Figure 1] and in the frequency domain [Figure 2].
When one wants to store the data of (i.e. reading the data onto a CD in this case) an infinite number of data points is not ideal -- in fact, it is impossible. Therefore, we must sample the data at the (typical) rate of . This will give us a periodic function which we will call is the sampling period. It is common to allow a sampling rate of twice the frequency at which a human can hear (i.e. 2 x 22 kHz) -- that means, kHz.
Recall from class that in order to sample the original function, , we need to use a delta function. In other words, the continuous function of can be written as [Figure 3]. As one may expect, in the frequency domain we should get the same plot as in Figure 2, but it should repeat. In the frequency domain, this can be expressed as [Figure 4].
As one may suspect, in order to get a more accurate function you must take more data points -- in other words, a higher sampling rate (i.e. 2x, 8x, etc. oversampling) leads to a more accurate collection of data. For this case, we are asked to looked a digital sampling, or 1x oversampling. In order to accomplish this, we will convolve our function from above with a Finite Impulse Response filter (FIR filter). Let's call it g(t and define it as where is the oversampling rate. In our case . Because we are dealing with digital sampling, the convolution will result in the original function [Figure 5].