LNA: Difference between revisions
(→HW#5) |
(→HW#5) |
||
| Line 5: | Line 5: | ||
PROBLEM STATEMENT: |
PROBLEM STATEMENT: |
||
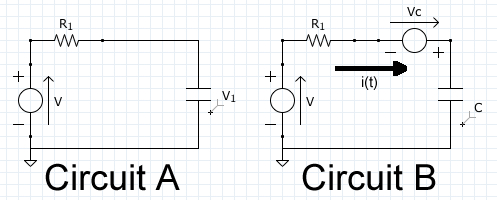
Solve for current i(t) in CIRCUIT A below using Laplace Transforms. |
Solve for current i(t) in CIRCUIT A below using Laplace Transforms. |
||
The two circuits (A and B below) are the same circuit. B is the same as A, only it shows are current when we use KVL and after we have moved the circuit into the "S" domain. |
|||
[[Image:Circuitben.jpg]] |
[[Image:Circuitben.jpg]] |
||
First, lets write each of the components into their Laplace form, go from the "t" to the "s" domain. Using KVL and assuming the current from ground through the voltage source>resister>capacitor>back to ground. |
|||
Voltage Source: <math>v(t)</math> -> - |
|||
<math>V_t</math>(0)/S |
|||
Resister: r -> R |
|||
Capacitor: c -> 1/(C*S) - <math>V_c</math>(0) Where <math>V_c</math> is the initial voltage of the cap. |
|||
Combining to portray the circuit B above using KVL gives: |
|||
Revision as of 09:07, 10 November 2009
Ben Henry LNA Homework
HW#5
The below problem, although simple, is done with variables so that values can be plugged in afterwords. Thus one can see how the problem progresses and see where the initial conditions end up at the end. PROBLEM STATEMENT: Solve for current i(t) in CIRCUIT A below using Laplace Transforms. The two circuits (A and B below) are the same circuit. B is the same as A, only it shows are current when we use KVL and after we have moved the circuit into the "S" domain.
First, lets write each of the components into their Laplace form, go from the "t" to the "s" domain. Using KVL and assuming the current from ground through the voltage source>resister>capacitor>back to ground.
Voltage Source: -> - (0)/S
Resister: r -> R
Capacitor: c -> 1/(C*S) - (0) Where is the initial voltage of the cap.
Combining to portray the circuit B above using KVL gives: