Coupled Oscillator: Coupled Mass-Spring System with Input

Setup State Space Equation

Problem Statement

Find an input function such that the lower mass, $m_1$, is stationary in the steady state. Find the equation of motion for the upper mass, $m_2$.

The use of one spring between the masses is just a simplification of a multi-spring system, so the possibility of being off-kilter is neglected and just the vertical forces are considered.

Problem Setup

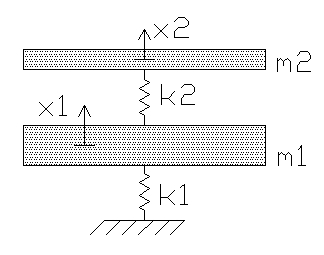
Initial Conditions and Values

$m_1=140kg\frac{}{}$

$k_1=108000\frac{N}{m}$

$m_2=80kg\frac{}{}$

$k_2=80000\frac{N}{m}$

Let the initial conditions be zero for the time being.

Force Equations

FBD for m2

FBD for m1

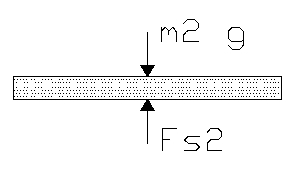
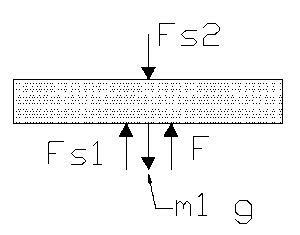
Sum of the forces in the x direction yields

For $m_1\frac{}{}$

$+\uparrow \sum F_{x_2}=m_2{\ddot{x}}_2$

$$\begin{gathered} \Rightarrow \\ {m}_2{\ddot{x}}_2=F_{s_2}-m_{2}g \end{gathered}$$

Since $F_s=-kx$

$$\begin{gathered} \Rightarrow \\ {\ddot{x}}_2=\frac{-k_2}{m_2}{x}_2-g \end{gathered}$$

And for $m_1\frac{}{}$

$+\uparrow \sum F_{x_1}=m_1{\ddot{x}}_1$

$$\begin{gathered} \Rightarrow \\ {m}_1{\ddot{x}}_1=F_{s_1}+F-m_{1}g-F_{s_2} \end{gathered}$$

Where $F\frac{}{}=F(t)$ is the input force

$$\begin{gathered} \Rightarrow \\ {\ddot{x}}_1=\frac{-k_1}{m_1}{x}_1+\frac{k_2}{m_1}{x}_2-g+\frac{F}{m_1} \end{gathered}$$

State Space Equation

The general form of the state equation is

$\underset{\_}{\dot{x}}(t)=\hat{A}\underset{\_}{x}(t)+\hat{C}\underset{\_}{u}(t)$

Where $\hat{M}$ denotes a matrix and $\underset{\_}{v}$ denotes a vector.

Let $x_1\frac{}{}$, ${\dot{x}}_1\frac{}{}$, $x_2\frac{}{}$, and $\dot{x_2}\frac{}{}$ be the state variables, then

$\left[\begin{array}{c}{\dot{x}}_1\\ {\ddot{x}}_1\\ {\dot{x}}_2\\ {\ddot{x}}_2\end{array}\right]=$ $\left[\begin{array}{cccc}0& 1& 0& 0\\ \frac{-k_1}{m_1}& 0& \frac{k_2}{m_1}& 0\\ 0& 0& 0& 1\\ 0& 0& \frac{-k_2}{m_2}& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ {\dot{x}}_1\\ x_2\\ {\dot{x}}_2\end{array}\right]+\left[\begin{array}{cccc}0& 0& 0& 0\\ -1& \frac{1}{m_1}& 0& 0\\ 0& 0& 0& 0\\ -1& 0& 0& 0\end{array}\right]\left[\begin{array}{c}g\\ F\\ 0\\ 0\end{array}\right]$