LNA

Ben Henry LNA Homework

HW#5

The below problem, although simple, is done with variables so values can be plugged in afterwords. Thus, one can see how the problem progresses and see where the initial conditions end up at the end.

---

PROBLEM STATEMENT:

Solve for current i(t) in CIRCUIT A below using Laplace Transforms. $V_{t}(0)=7v$, Failed to parse (syntax error): {\displaystyle r=40Ω} , $c=2F$, $V_{c}(0)=3v.$

The two circuits (A and B below) are the same circuit. B is the same as A, only it shows are current when we use KVL and after we have moved the circuit into the "S" domain.

---

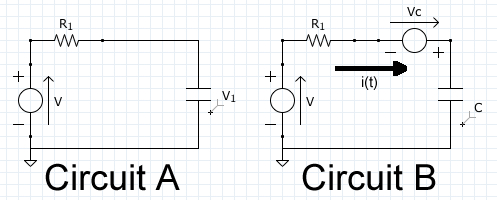
Write Each Components in Laplace Form

Go from the "t" to the "s" domain right off the bat. Using KVL and assuming the current from ground through the voltage source>resister>capacitor>back to ground.

Voltage Source in Volts: $v(t)$ -> - $V_{t}$(0)/S

Resister in OHMs: r -> R

Capacitor in Farads: c -> 1/(CS) - $V_{c}$(0) Where $V_{c}$ is the initial voltage of the cap.

---

Apply KVL to Circuit B in S Domain

-${\tfrac {V_{t}(0)}{S}}$+I(s)(R+${\tfrac {1}{CS}}$)-$V_{c}$(0)=0

---

Solving for I(S)

$I(S)={\cfrac {V_{t}(0)+V_{c}(0)}{S(R+{\tfrac {1}{CS}})}}={\cfrac {(V_{t}(0)+V_{c}(0))}{SR+{\tfrac {1}{C}}}}{\frac {\tfrac {1}{R}}{\tfrac {1}{R}}}={\cfrac {\tfrac {V_{t}(0)+V_{c}(0)}{R}}{S+{\tfrac {1}{RC}}}}$

---

Performing the inverse Laplace

$L^{-1}(I(S))=L^{-1}({\cfrac {\tfrac {V_{t}(0)+V_{c}(0)}{R}}{S+{\tfrac {1}{RC}}}})=i(t)={\frac {V_{t}(0)+V_{c}(0)}{r}}e^{(-{\tfrac {1}{rC}}t)}$

---

Apply Initial Conditions

$V_{t}(0)=7v$

Failed to parse (SVG with PNG fallback (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = 40 Ω}

$c=2F$

$V_{c}(0)=3v$

$i(t)={\frac {V_{t}(0)+V_{c}(0)}{r}}e^{(-{\tfrac {1}{rC}}t)}={\frac {7+3}{40}}e^{(-{\tfrac {1}{40*2}}t)}={\tfrac {1}{4}}e^{-{\tfrac {1}{40}}t}$

HW#6 "Initial and Final Value Theorems"

Initial Value Theorem

$\lim _{s\to \infty }sF(s)=f(0)$

Applying to our equation for i(t) we have

IVT of i(t)=$\lim _{s\to \infty }sI(s)=s({\cfrac {\tfrac {V_{t}(0)+V_{c}(0)}{R}}{S+{\tfrac {1}{RC}}}})=({\tfrac {\tfrac {1}{s}}{\tfrac {1}{s}}})({\cfrac {s({\tfrac {V_{t}(0)+V_{c}(0))}{R}}}{S+{\tfrac {1}{RC}}}})=({\cfrac {\tfrac {V_{t}(0)+V_{c}(0)}{R}}{1+{\tfrac {1}{sRC}}}})=({\cfrac {\tfrac {7+3}{40}}{1+{\tfrac {1}{s40*2}}}})=({\cfrac {\tfrac {1}{4}}{1+0}})={\tfrac {1}{4}}$

Final Value Theorem

$\lim _{s\to 0}sF(s)=f(0)$

Applying to our equation for i(t) we have

FVT of i(t)=$\lim _{s\to 0}sI(s)=s({\cfrac {\tfrac {V_{t}(0)+V_{c}(0)}{R}}{S+{\tfrac {1}{RC}}}})=({\cfrac {\tfrac {s(V_{t}(0)+V_{c}(0))}{R}}{S+{\tfrac {1}{RC}}}})=({\cfrac {\tfrac {0(V_{t}(0)+V_{c}(0))}{R}}{0+{\tfrac {1}{RC}}}})=0$

With this result of zero "0" we know that eventually the current will go to zero. After examining the circuit, it is quite obvious that the current will go to zero once the capacitor is charged.

If the voltage v(t) is desired instead

If in either the IVT or FVT you want to find v(t) instead of i(t), simply multiply the current i(t) by the resistance R. e.g. $V=IR,sov(t)=R(i(t))=R({\cfrac {\tfrac {V_{t}(0)+V_{c}(0)}{R}}{S+{\tfrac {1}{RC}}}}$