Sampling - HW7

Max Woesner

Back to my Home Page

Homework #7 - Sampling

Problem Statement
Figure out what happens if your sampled signal, $x(t)$, has frequency components only for $\frac{f_s}{2}<f<f_s$. Can you recover the original signal from it? If so, find the expression for $x(t)$ in terms of $x(nT)$.

Solution
For frequency components $\frac{f_s}{2}<f<f_s$, our sampled signal $x(t)$ in the frequency domain, or $X(f)$, is going to look like this.



After sampling with frequency $f_s$, the signal is going to be shifted over by $\frac{1}{T}$, since $f_s=\frac{1}{T}$. It will look like this.



To recover the original signal $x(t)$, we need to a use bandpass filter to filter out the parts we don't want, as indicated by the red line in the figure below. (Note: not to scale.)



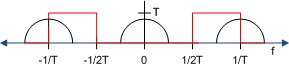
This leaves us with the original signal, as shown below.



The transfer function of the bandpass filter that will accomplish this for us is $H(f)=\{\begin{array}{ll}T,& \frac{1}{2T}<|f|<\frac{1}{T}\\ 0,& \text{ else }\end{array}$

To find the expression for $h(t)$, or the expression for the bandpass filter in the time domain, we can take the inverse Fourier transform of $H(f)$.

$$\begin{gathered} h(t)={{ℱ}}^{-1}[H(f)]=\underset{-\frac{1}{T}}{\overset{-\frac{1}{2T}}{\int }}T{e}^{j2\pi ft}df \\ +\underset{\frac{1}{2T}}{\overset{\frac{1}{T}}{\int }}T{e}^{j2\pi ft}df=\frac{T{e}^{j2\pi ft}}{j2\pi t}{|}_{f=-\frac{1}{T}}^{-\frac{1}{2T}}+ \\ \frac{T{e}^{j2\pi ft}}{j2\pi t}{|}_{f=\frac{1}{2T}}^{\frac{1}{T}} \end{gathered}$$

$$\begin{gathered} h(t)=T\frac{e^{-j\pi t/T}-e^{-j2\pi t/T}}{j2(\pi t)} \\ + \\ T\frac{e^{j2\pi t/T}-e^{j\pi t/T}}{j2(\pi t)}=\frac{T}{j2}\left[\frac{e^{-j\pi t/T}-e^{-j2\pi t/T}+e^{j2\pi t/T}-e^{j\pi t/T}}{\pi t}\right] \end{gathered}$$

$$\begin{gathered} h(t)=\frac{T}{j2}\left[\frac{-e^{j\pi t/T}+e^{-j\pi t/T}+e^{j2\pi t/T}-e^{-j2\pi t/T}}{\pi t}\right]=\frac{T}{j2}\left[\frac{e^{j2\pi t/T}-e^{-j2\pi t/T}}{\pi t}\right]- \\ \frac{T}{j2}\left[\frac{e^{j\pi t/T}-e^{-j\pi t/T}}{\pi t}\right] \end{gathered}$$

Recall $sin(\theta )=\frac{1}{j2}(e^{j\theta }-e^{-j\theta })$, so

$$\begin{gathered} h(t)=\frac{T}{j2}\left[\frac{e^{j2\pi t/T}-e^{-j2\pi t/T}}{\pi t}\right]- \\ \frac{T}{j2}\left[\frac{e^{j\pi t/T}-e^{-j\pi t/T}}{\pi t}\right]=\frac{T}{\pi t}sin\left(\frac{2\pi t}{T}\right) \\ - \\ \frac{T}{\pi t}sin\left(\frac{\pi t}{T}\right)=\frac{2sin\left(\frac{2\pi t}{T}\right)}{\frac{2\pi t}{T}} \\ - \\ \frac{sin\left(\frac{\pi t}{T}\right)}{\frac{\pi t}{T}} \end{gathered}$$

Also recall $sinc(\theta )=\frac{sin(\pi \theta )}{\pi \theta }$, so

$$\begin{gathered} h(t)=\frac{2sin\left(\frac{2\pi t}{T}\right)}{\frac{2\pi t}{T}} \\ - \\ \frac{sin\left(\frac{\pi t}{T}\right)}{\frac{\pi t}{T}}=2sinc\left(\frac{2t}{T}\right)-sinc\left(\frac{t}{T}\right) \end{gathered}$$

Now that we know $h(t)$, we can find $x(t)$ by convolving the function for $x(t)$ after sampling, or $\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}x(nT)\delta (t-nT)$, with $h(t)$.

$$\begin{gathered} x(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}x(nT)\delta (t-nT)*\left[2sinc\right(\frac{2t}{T})-sinc(\frac{t}{T}\left)\right]=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}x(nT)\left[2sinc\right(\frac{2(t-nT)}{T}) \\ - \\ sinc(\frac{t-nT}{T}\left)\right] \end{gathered}$$

Or, if you prefer, $$\begin{gathered} x(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}x(nT)[\frac{2sin\left(\frac{2\pi (t-nT)}{T}\right)}{\frac{2\pi (t-nT)}{T}} \\ - \\ \frac{sin\left(\frac{\pi (t-nT)}{T}\right)}{\frac{\pi (t-nT)}{T}}] \end{gathered}$$

Alternatively, a different bandpass filter can be used that will simplify the math we have to do, such as the one indicated by the red line in the figure below. (Note: not to scale.)



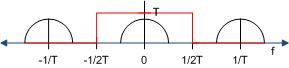
Leaving us with the signal shown below.



The transfer function of this bandpass filter is $H(f)=\{\begin{array}{ll}T,& |f|<\frac{1}{2T}\\ 0,& \text{ else }\end{array}$

To find the expression for $h(t)$, or the expression for the bandpass filter in the time domain, we can take the inverse Fourier transform of $H(f)$.

$$\begin{gathered} h(t)={{ℱ}}^{-1}[H(f)]=\underset{-\frac{1}{2T}}{\overset{\frac{1}{2T}}{\int }}T{e}^{j2\pi ft}df \\ =\frac{T{e}^{j2\pi ft}}{j2\pi t}{|}_{f=-\frac{1}{2T}}^{\frac{1}{2T}}=\frac{T}{j2}\left[\frac{e^{j\pi t/T}-e^{-j\pi t/T}}{\pi t}\right] \end{gathered}$$

Recall again that $sin(\theta )=\frac{1}{j2}(e^{j\theta }-e^{-j\theta })$, so

$$\begin{gathered} h(t)=\frac{T}{j2}\left[\frac{e^{j\pi t/T}-e^{-j\pi t/T}}{\pi t}\right]=\frac{T}{\pi t}sin\left(\frac{\pi t}{T}\right) \\ =\frac{sin\left(\frac{\pi t}{T}\right)}{\frac{\pi t}{T}} \end{gathered}$$

Also recall again that $sinc(\theta )=\frac{sin(\pi \theta )}{\pi \theta }$, so

$h(t)=\frac{sin\left(\frac{\pi t}{T}\right)}{\frac{\pi t}{T}}=sinc\left(\frac{t}{T}\right)$

Now that we know $h(t)$, we can find $x(t)$ by convolving the function for $x(t)$ after sampling, or $\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}x(nT)\delta (t-nT)$, with $h(t)$.

$x(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}x(nT)\delta (t-nT)*\left[sinc\right(\frac{t}{T}\left)\right]=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}x(nT)(sinc(\frac{t-nT}{T})$

Or, if you prefer, $x(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}x(nT)\left[\frac{sin\left(\frac{\pi (t-nT)}{T}\right)}{\frac{\pi (t-nT)}{T}}\right]$