Coupled Oscillator: horizontal Mass-Spring

Problem Statement

Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes and eigenvectors of the system.

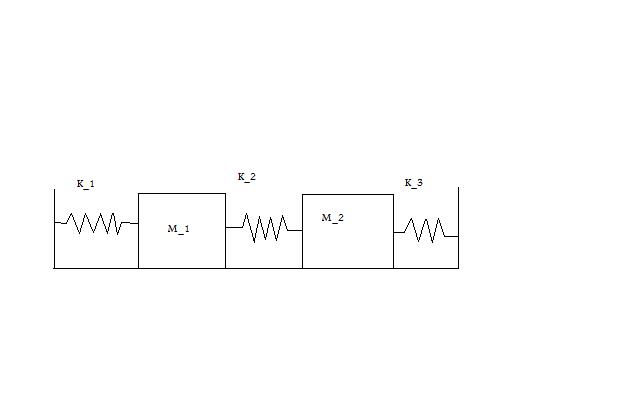
Initial Conditions:

$m_1=10kg$

$m_2=10kg$

$k1=25N/m$

$k2=75N/m$

$k3=50N/m$

Equations for M_1

$\begin{array}{rl}F& =ma\\ F& =m\ddot{x}\\ -k_1{x}_1-k_2(x_1{x}_2)& =m_1\ddot{x_1}\\ -\frac{k_1{x}_1}{m_1}-\frac{k_2(x_1-x_2)}{m_1}& =m_1\ddot{x_1}\\ -\frac{k_1{x}_1}{m_1}-\frac{k_2(x_1-x_2)}{m_1}& =\ddot{x_1}\\ -\frac{k_1+k_2}{m_1}{x}_1+\frac{k_2}{m_1}{x}_2& =\ddot{x_1}\\ \end{array}$

Equations for M_2

$\begin{array}{rl}F& =ma\\ F& =m\ddot{x}\\ -k_2(x_2-x_1)& =m_2\ddot{x_2}\\ \frac{-k_2(x_2-x_1)}{m_2}& =\ddot{x_2}\\ -\frac{k_2}{m_2}{x}_2+\frac{k_2}{m_2}{x}_1& =\ddot{x_2}\\ \end{array}$

Additional Equations

$\dot{x_1}=\dot{x_1}$

$\dot{x_2}=\dot{x_2}$

State Equations

$\left[\begin{array}{c}\dot{x_1}\\ \ddot{x_1}\\ \dot{x_2}\\ \ddot{x_2}\end{array}\right]$ = $\left[\begin{array}{cccc}0& 1& 0& 0\\ \frac{(k_1-k_2)}{m_1}& 0& \frac{-k_1}{m_1}& 0\\ 0& 0& 0& 1\\ \frac{k_1}{m_2}& 0& \frac{(k_1+k_2)}{m_2}& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ {\dot{x}}_1\\ x_2\\ {\dot{x}}_2\end{array}\right]+\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]$

With the numbers...

$\left[\begin{array}{c}\dot{x_1}\\ \ddot{x_1}\\ \dot{x_2}\\ \ddot{x_2}\end{array}\right]$ = $\left[\begin{array}{cccc}0& 1& 0& 0\\ \frac{(-50N/m)}{10kg}& 0& \frac{-25N/m}{10kg}& 0\\ 0& 0& 0& 1\\ \frac{25N/m}{10kg}& 0& \frac{(100N/m)}{10kg}& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ {\dot{x}}_1\\ x_2\\ {\dot{x}}_2\end{array}\right]$

Eigen Values

Once you have your equations of equilibrium in matrix form you can plug them into a calculator or a computer program that will give you the eigen values automatically. This saves you a lot of hand work. Here's what you should come up with for this particular problem given these initial conditions.

Given

$m_1=10kg$

$m_2=10kg$

$k_1=25\frac{N}{m}$

$k_2=50\frac{N}{m}$

We now have

$\left[\begin{array}{c}\dot{x_1}\\ \ddot{x_1}\\ \dot{x_2}\\ \ddot{x_2}\end{array}\right]=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ \dot{x_1}\\ x_2\\ \dot{x_2}\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]$

From this we get

${\lambda }_1=$

${\lambda }_2=$

${\lambda }_3=$

${\lambda }_4=$