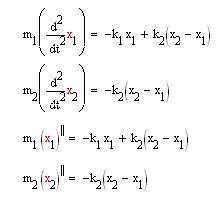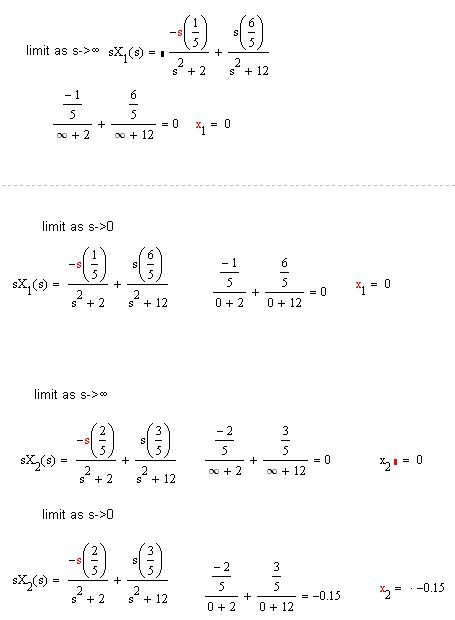Laplace Transforms: Coupled Springs

Jaymin Joseph

Part 1: Laplace Transform

Problem Statement: (Equations typed out in mathcad and uploaded as images)

This is a system of two masses connected by two springs with spring constants k1 and k2. This system is shown below.

From the FBD, the equations of motion can be determined to be as follows:

To solve the system let K1=6 k2=4, m1=1, m2=1 and x1(0)=0, x1'(0)=1 x2(0)=0, x2'(0)=-2

Part 2: Inverse Laplace Transform

Part 3: Initial-Value & Final-Value Theorem

By definition, the Initial-Value Theorem is,

$\lim _{s\rightarrow \infty }sX(s)=x(0)\,$

and the Final-Value Theorem is,

$\lim _{s\rightarrow 0}sX(s)=x(\infty )\,$

Applying this to the system i get the following.

Part 4: Bode Plot

Part 5:Magnitude Frequency Response

Part 6: Convolution

the definition of convolution of two functions is,

$y(t)=f(t)*h(t)=\int _{-\infty }^{\infty }{f(\tau )h(t-\tau )d\tau }=\int _{\infty }^{-\infty }{f(t-\tau )h(\tau )d\tau }$

applying the definition of convolution to this system we get: