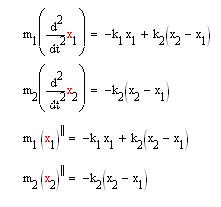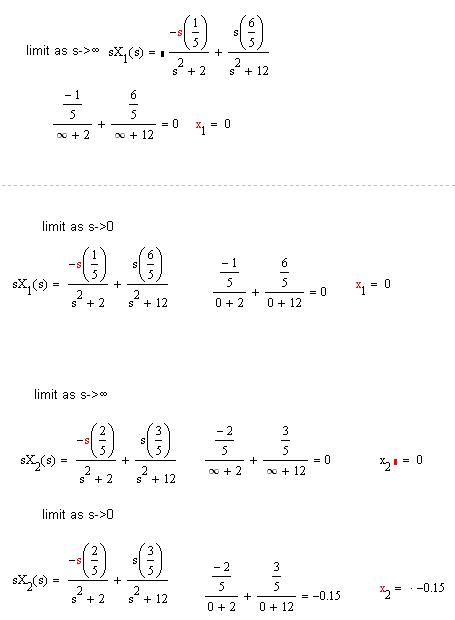Laplace Transforms: Coupled Springs: Difference between revisions
No edit summary |
No edit summary |
||
| Line 52: | Line 52: | ||
'''Part 6: Convolution''' | '''Part 6: Convolution''' | ||
the definition of convolution of two functions is, | |||
<math>y(t)=f(t)*h(t)=\int_{-\infty}^{\infty}{f(\tau)h(t-\tau)d\tau}=\int_{\infty}^{-\infty}{f(t-\tau)h(\tau)d\tau}</math> | |||
applying the definition of convolution to this system we get: | |||
[[Image:7.jpg]] | |||
Latest revision as of 16:34, 10 December 2009
Jaymin Joseph
Part 1: Laplace Transform
Problem Statement: (Equations typed out in mathcad and uploaded as images)
This is a system of two masses connected by two springs with spring constants k1 and k2.
This system is shown below.
From the FBD, the equations of motion can be determined to be as follows:
To solve the system let K1=6 k2=4, m1=1, m2=1 and x1(0)=0, x1'(0)=1 x2(0)=0, x2'(0)=-2
Part 2: Inverse Laplace Transform
Part 3: Initial-Value & Final-Value Theorem
By definition, the Initial-Value Theorem is,
and the Final-Value Theorem is,
Applying this to the system i get the following.
Part 4: Bode Plot
Part 5:Magnitude Frequency Response
Part 6: Convolution
the definition of convolution of two functions is,
applying the definition of convolution to this system we get: