Coupled Oscillator: Hellie

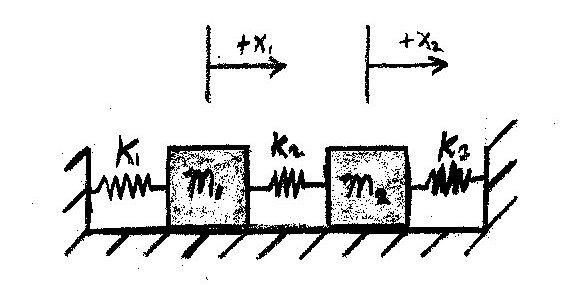
Problem Statement

Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes of the system.

Initial Conditions:

$m_{1}=15kg\,$

$m_{2}=15kg\,$

$k1=100N/m\,$

$k2=150N/m\,$

$k3=100N/m\,$

State Equations

${\begin{bmatrix}{\dot {x_{1}}}\\{\ddot {x_{1}}}\\{\dot {x_{2}}}\\{\ddot {x_{2}}}\end{bmatrix}}\,$ = ${\begin{bmatrix}0&1&0&0\\{\frac {(k_{1}-k_{2})}{m_{1}}}&0&{\frac {-k_{1}}{m_{1}}}&0\\0&0&0&1\\{\frac {-k_{1}}{m_{2}}}&0&{\frac {(k_{1}+k_{2})}{m_{2}}}&0\end{bmatrix}}{\begin{bmatrix}x_{1}\\{\dot {x}}_{1}\\x_{2}\\{\dot {x}}_{2}\end{bmatrix}}+{\begin{bmatrix}0&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}}{\begin{bmatrix}0\\0\\0\\0\end{bmatrix}}$

With the numbers...

${\begin{bmatrix}{\dot {x_{1}}}\\{\ddot {x_{1}}}\\{\dot {x_{2}}}\\{\ddot {x_{2}}}\end{bmatrix}}\,$ = ${\begin{bmatrix}0&1&0&0\\{\frac {(-50N/m)}{15kg}}&0&{\frac {-100N/m}{15kg}}&0\\0&0&0&1\\{\frac {100N/m}{15kg}}&0&{\frac {(250N/m)}{15kg}}&0\end{bmatrix}}{\begin{bmatrix}x_{1}\\{\dot {x}}_{1}\\x_{2}\\{\dot {x}}_{2}\end{bmatrix}}$

Eigenmodes

There are two eigenmodes for the system

1) m1 and m2 oscillating together

2) m1 and m2 oscillating at exactly a half period difference

Solve Using the Matrix Exponential

$e^{At}={\mathcal {L}}^{-1}\left\{[SI-A]^{-1}\right\}\,$

$[SI-A]\,$ = ${\begin{bmatrix}S&1&0&0\\{\frac {(-50N/m)}{15kg}}&S&{\frac {-100N/m}{15kg}}&0\\0&0&S&1\\{\frac {100N/m}{15kg}}&0&{\frac {(250N/m)}{15kg}}&S\end{bmatrix}}$

$[SI-A]^{-1}=\,$

${\mathcal {L}}^{-1}\left\{[SI-A]^{-1}\right\}=\,$

Written by: Andrew Hellie