Coupled Oscillator: Hellie

Problem Statement

Write up on the Wiki a solution of a coupled oscillator problem like the coupled pendulum. Use State Space methods. Describe the eigenmodes of the system.

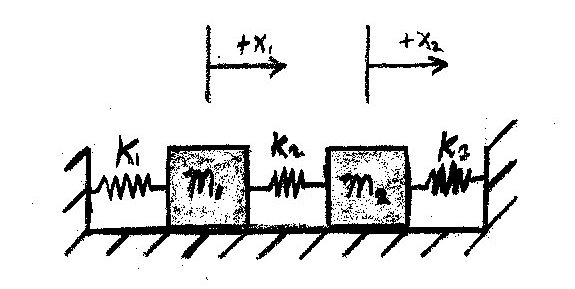
Initial Conditions:

$m_1=10kg$

$m_2=10kg$

$k1=100N/m$

$k2=150N/m$

$k3=100N/m$

State Equations

$\left[\begin{array}{c}\dot{x_1}\\ \ddot{x_1}\\ \dot{x_2}\\ \ddot{x_2}\end{array}\right]$ = $\left[\begin{array}{cccc}0& 1& 0& 0\\ \frac{(k_1-k_2)}{m_1}& 0& \frac{-k_1}{m_1}& 0\\ 0& 0& 0& 1\\ \frac{-k_1}{m_2}& 0& \frac{(k_1+k_2)}{m_2}& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ {\dot{x}}_1\\ x_2\\ {\dot{x}}_2\end{array}\right]+\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]$

With the numbers...

$\left[\begin{array}{c}\dot{x_1}\\ \ddot{x_1}\\ \dot{x_2}\\ \ddot{x_2}\end{array}\right]$ = $\left[\begin{array}{cccc}0& 1& 0& 0\\ \frac{(-50N/m)}{10kg}& 0& \frac{-100N/m}{10kg}& 0\\ 0& 0& 0& 1\\ \frac{-100N/m}{10kg}& 0& \frac{(250N/m)}{10kg}& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ {\dot{x}}_1\\ x_2\\ {\dot{x}}_2\end{array}\right]$

$\left[\begin{array}{c}\dot{x_1}\\ \ddot{x_1}\\ \dot{x_2}\\ \ddot{x_2}\end{array}\right]$ = $\left[\begin{array}{cccc}0& 1& 0& 0\\ -5& 0& -10& 0\\ 0& 0& 0& 1\\ -10& 0& 25& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ {\dot{x}}_1\\ x_2\\ {\dot{x}}_2\end{array}\right]$

Eigenvalues

${\lambda }_1=-5.29412$

${\lambda }_2=2.83333i$

${\lambda }_3=-2.83333i$

${\lambda }_4=0$

Eigenvectors

$k_1=\left[\begin{array}{c}-.05379\\ .28475\\ .17764\\ -.94046\end{array}\right]$

$k_2=\left[\begin{array}{c}-.31854i\\ .90253\\ -.09645i\\ .27326\end{array}\right]$

$k_3=\left[\begin{array}{c}.31854i\\ .90253\\ .09645i\\ .27326\end{array}\right]$

$k_4=\left[\begin{array}{c}-.05379\\ -.28475\\ .17764\\ .94046\end{array}\right]$

Standard Equation

$x=c_1{k}_1{e}^{{\lambda }_{1}t}+c_2{k}_2{e}^{{\lambda }_{2}t}+c_3{k}_3{e}^{{\lambda }_{3}t}+c_4{k}_4{e}^{{\lambda }_{4}t}$

$x=c_1$$\left[\begin{array}{c}-.05379\\ .28475\\ .17764\\ -.94046\end{array}\right]$$e^{-5.29412}+c_2$$\left[\begin{array}{c}-.31854i\\ .90253\\ -.09645i\\ .27326\end{array}\right]$$e^{2.83333i}+c_3$$\left[\begin{array}{c}.31854i\\ .90253\\ .09645i\\ .27326\end{array}\right]$$e^{-2.83333i}+c_4$$\left[\begin{array}{c}-.05379\\ -.28475\\ .17764\\ .94046\end{array}\right],$$e^0$

Eigenmodes

There are two eigenmodes for the system

1) m1 and m2 oscillating together

2) m1 and m2 oscillating at exactly a half period difference

Solve Using the Matrix Exponential

$e^{At}={{ℒ}}^{-1}\{[SI-A{]}^{-1}\}$

$[SI-A]$ = $\left[\begin{array}{cccc}S& 1& 0& 0\\ \frac{(-50N/m)}{15kg}& S& \frac{-100N/m}{15kg}& 0\\ 0& 0& S& 1\\ \frac{100N/m}{15kg}& 0& \frac{(250N/m)}{15kg}& S\end{array}\right]$

$[SI-A{]}^{-1}=$

${{ℒ}}^{-1}\{[SI-A{]}^{-1}\}=$

Written by: Andrew Hellie